
BARBIER Matthieu
- Centre for Biodiversity Theory and Modelling, CNRS, Moulis, France
- Coexistence, Community ecology, Competition, Food webs, Foraging, Interaction networks, Population ecology, Spatial ecology, Metacommunities & Metapopulations, Theoretical ecology
- recommender
Recommendations: 3
Reviews: 2
Recommendations: 3
Beyond variance: simple random distributions are not a good proxy for intraspecific variability in systems with environmental structure
Two paradigms for intraspecific variability
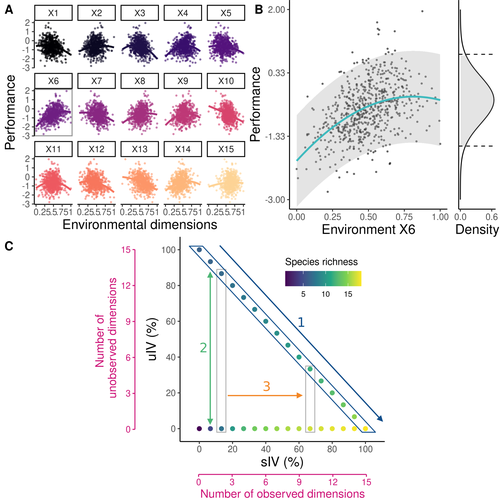
Recommended by Matthieu Barbier based on reviews by Simon Blanchet and Bart HaegemanCommunity ecology usually concerns itself with understanding the causes and consequences of diversity at a given taxonomic resolution, most classically at the species level. Yet there is no doubt that diversity exists at all scales, and phenotypic variability within a taxon can be comparable to differences between taxa, as observed from bacteria to fish and trees. The question that motivates an active and growing body of work (e.g. Raffard et al 2019) is not so much whether intraspecific variability matters, but what we get wrong by ignoring it and how to incorporate it into our understanding of communities. There is no established way to think about diversity at multiple nested taxonomic levels, and it is tempting to summarize intraspecific variability simply by measuring species mean and variance in any trait and metric.
In this study, Girard-Tercieux et al (2023a) propose that, to understand its impact on community-level outcomes and in particular on species coexistence, we should carefully distinguish between two ways of thinking about intraspecific variability:
-"unstructured" variation, where every individual's features are like an independent random draw from a species-specific distribution, for instance, due to genetic lottery and developmental accidents
-"structured" variation that is due to each individual encountering a different but enduring microenvironment.
The latter type of variability may still appear complex and random-like when the environment is high-dimensional (i.e. multifaceted, with many different factors contributing to each individual's performance and development). Thus, it is not necessarily "structured" in the sense of being easily understood -- we may need to measure more aspects of the environment than is practical if we want to fully predict these variations.
What distinguishes this "structured" variability is that it is, in a loose sense, inheritable: individuals from the same species that grow in the same microenvironment will have the same performance, in a repeatable fashion. Thus, if each species is best at exploiting at least a fraction of environmental conditions, it is likely to avoid extinction by competition, except in the unlucky case of no propagule reaching any of the favorable sites.
By contrast, drawing each individual's preferences and performance randomly at each generation (from its own species distribution, but independently from other and past individuals) leads to stochastic dynamics, so-called ecological drift, that easily induce a large number of species extinctions.
The core intuition, that the complex spatial structure and high-dimensional nature of the environment plays a key explanatory role in species coexistence, is a running thread through several of the authors' work (e.g. Clark et al 2010), clearly inspired by their focus on tropical forests. This study, by tackling the question of intraspecific determinants of interspecific outcomes, makes a compelling addition to this line of investigation, coming as a theoretical companion to a more data-oriented study (Girard-Tercieux et al 2023b). But I believe it raises a question that is even broader in scope.
This kind of intraspecific variability, due to different individuals growing in different microenvironments, is perhaps most relevant for trees and other sessile organisms, but the distinction made here between "unstructured" and "structured" variability can likely be extended to many other ecological settings.
In my understanding, what matters most in "structured" variability is not so much it stemming from a fixed environment, but rather it being maintained across generations, rather than possibly lost by drift. This difference between variability in the form of "frozen" randomness and in the form of stochastic drift over time is highly relevant in other theoretical fields (e.g. in physics, where it is the difference between a disordered solid and a liquid), and thus, I expect that it is a meaningful distinction to make throughout community ecology.
References
James S. Clark, David Bell, Chengjin Chu, Benoit Courbaud, Michael Dietze, Michelle Hersh, Janneke HilleRisLambers et al. (2010) "High‐dimensional coexistence based on individual variation: a synthesis of evidence." Ecological Monographs 80, no. 4 : 569-608. https://doi.org/10.1890/09-1541.1
Camille Girard-Tercieux, Ghislain Vieilledent, Adam Clark, James S. Clark, Benoît Courbaud, Claire Fortunel, Georges Kunstler, Raphaël Pélissier, Nadja Rüger, Isabelle Maréchaux (2023a) "Beyond variance: simple random distributions are not a good proxy for intraspecific variability in systems with environmental structure." bioRxiv, ver. 4 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2022.08.06.503032
Camille Girard‐Tercieux, Isabelle Maréchaux, Adam T. Clark, James S. Clark, Benoît Courbaud, Claire Fortunel, Joannès Guillemot et al. (2023b) "Rethinking the nature of intraspecific variability and its consequences on species coexistence." Ecology and Evolution 13, no. 3 : e9860. https://doi.org/10.1002/ece3.9860
Allan Raffard, Frédéric Santoul, Julien Cucherousset, and Simon Blanchet. (2019) "The community and ecosystem consequences of intraspecific diversity: A meta‐analysis." Biological Reviews 94, no. 2: 648-661. https://doi.org/10.1111/brv.12472

Inferring macro-ecological patterns from local species' occurrences
Upscaling the neighborhood: how to get species diversity, abundance and range distributions from local presence/absence data
Recommended by Matthieu Barbier based on reviews by Kevin Cazelles and 1 anonymous reviewerHow do you estimate the biodiversity of a whole community, or the distribution of abundances and ranges of its species, from presence/absence data in scattered samples?
It all starts with the collector's dilemma: if you double the number of samples, you will not get double the number of species, since you will find many of the same common species, and only a few new rare ones.
This non-additivity has prompted many ecologists to study the Species-Area Relationship. A common theoretical approach has been to connect this spatial pattern to the overall distribution of how common or rare a species can be. At least since Fisher's celebrated log-series [1], ecologists have been trying to, first, infer the shape of the Species Abundance Distribution, and then, use it to predict how many species should be found in a given area or a given number of samples. This has found many applications, from microbial communities to tropical forests, from estimating the number of yet-unknown species to predicting how much biodiversity may be lost if a fraction of the habitat is removed.
In this elegant work, Tovo et al. [2] propose a method that starts only from presence/absence data over a number of samples, and provides the community's diversity, as well as its abundance and range size distributions. This method is simple, analytically explicit, and accurate: the authors test it on the classic Pasoh and Barro Colorado Island tropical forest datasets, and on simulated data. They make a very laudable effort in both explaining its theoretical underpinnings, and proposing a straightforward step-by-step guide to applying it to data.
The core of Tovo et al's method is a simple property: the scale invariance of the Negative Binomial (NB) distribution. Subsampling from a NB gives another NB, where a single parameter has changed. Therefore, if the Species Abundance Distribution is close enough to some NB (which is flexible enough to accommodate all the data here), we can estimate how this parameter changes when going from (1) a single sample to (2) all the available samples, and from there, extrapolate to (3) the entire community.
This principle was first applied by the authors in a previous study [3] that required abundance data in the samples, rather than just presence/absence. Given that binary occurrence data is far more available in a variety of empirical settings, this extension is worthwhile (including its new predictions on range size distributions), and it deserves to be widely known and tested.
ADDITIONAL COMMENTS
1) To explain the novelty of the authors' contribution, it is useful to look at competing techniques.
Some ""parametric"" approaches try to infer the whole-community Species Abundance Distribution (SAD) by guessing its functional form (Gaussian, power-law, log-series...) and fitting its parameters from sampled data. The issue is that this distribution shape may not remain in the same family as we increase the sampling effort or area, so the regression problem may not be well-defined. This is where the Negative Binomial's scale invariance is useful.
Other ""non-parametric"" approaches have renounced guessing the whole SAD: they simply try to approximate of its tail of rare species, by looking at how many species are found in only one (or a few) samples. From this, they derive an estimate of biodiversity that is agnostic to the rest of the SAD. Tovo et al. [2] show the issue with these approaches: they extrapolate from the properties of individual samples to the whole community, but do not properly account for the bias introduced by the amount of sampling (the intermediate scale (2) in the summary above).
2) The main condition for all such approaches to work is well-mixedness: each sample should be sufficiently like a lot drawn from the same skewed lottery. As long as that condition applies, finding the best approach is a theoretical matter of probabilities and combinatorics that may, in time, be given a definite answer.
The authors also show that ""well-mixed"" is not as restrictive as it sounds: the method works both on real data (which is never perfectly mixed) and on simulations where species are even more spatially clustered than the empirical data. In addition, the Negative Binomial's scale invariance entails that, if it works well enough at some spatial scale, it will also work at all higher scales (until one reaches the edges of the sufficiently-well-mixed community)
3) One may ask: why the Negative Binomial as a Species Abundance Distribution?
If one wishes for some dynamical explanation, the Negative Binomial can be derived from neutral birth and death process with immigration, as shown by the authors in [3]. But to be applied to data, it should only be able to approximate the empirical distribution well enough (at all relevant scales). Depending on one's taste, this type of probabilistic approaches can be interpreted as:
- purely phenomenological, describing only the observational process of sampling from an existing state of affairs, not the ecological processes that gave rise to that state.
- a null model, from which everything in practice is expected to deviate to some extent.
- or a way to capture the statistical forces that tend to induce stable relationships between different patterns (as long as no ecological process opposes them strongly enough).
References
[1] Fisher, R. A., Corbet, A. S., & Williams, C. B. (1943). The relation between the number of species and the number of individuals in a random sample of an animal population. The Journal of Animal Ecology, 42-58. doi: 10.2307/1411
[2] Tovo, A., Formentin, M., Suweis, S., Stivanello, S., Azaele, S., & Maritan, A. (2019). Inferring macro-ecological patterns from local species' occurrences. bioRxiv, 387456, ver. 2 peer-reviewed and recommended by PCI Ecol. doi: 10.1101/387456
[3] Tovo, A., Suweis, S., Formentin, M., Favretti, M., Volkov, I., Banavar, J. R., Azaele, S., & Maritan, A. (2017). Upscaling species richness and abundances in tropical forests. Science Advances, 3(10), e1701438. doi: 10.1126/sciadv.1701438
When higher carrying capacities lead to faster propagation
When the dispersal of the many outruns the dispersal of the few
Recommended by Matthieu Barbier based on reviews by Yuval Zelnik and 1 anonymous reviewerAre biological invasions driven by a few pioneers, running ahead of their conspecifics? Or are these pioneers constantly being caught up by, and folded into, the larger flux of propagules from the established populations behind them?
In ecology and beyond, these two scenarios are known as "pulled" and "pushed" fronts, and they come with different expectations. In a pushed front, invasion speed is not just a matter of how good individuals are at dispersing and settling new locations. It becomes a collective, density-dependent property of population fluxes. And in particular, it can depend on the equilibrium abundance of the established populations inside the range, i.e. the species’ carrying capacity K, factoring in its abiotic environment and biotic interactions.
This realization is especially important because it can flip around our expectations about which species expand fast, and how to manage them. We tend to think of initial colonization and long-term abundance as two independent axes of variation among species or indeed as two ends of a spectrum, in the classic competition-colonization tradeoff [1]. When both play into invasion speed, good dispersers might not outrun good competitors. This is useful knowledge, whether we want to contain an invasion or secure a reintroduction.
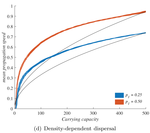
In their study "When higher carrying capacities lead to faster propagation", Haond et al [2] combine mathematical analysis, Individual-Based simulations and experiments to show that various mechanisms can cause pushed fronts, whose speed increases with the carrying capacity K of the species. Rather than focus on one particular angle, the authors endeavor to demonstrate that this qualitative effect appears again and again in a variety of settings.
It is perhaps surprising that this notable and general connection between K and invasion speed has managed to garner so little fame in ecology. A large fraction of the literature employs the venerable Fisher-KPP reaction-diffusion model, which combines local logistic growth with linear diffusion in space. This model has prompted both considerable mathematical developments [3] and many applications to modelling real invasions [4]. But it only allows pulled fronts, driven by the small populations at the edge of a species range, with a speed that depends only on their initial growth rate r.
This classic setup is, however, singular in many ways. Haond et al [2] use it as a null model, and introduce three mechanisms or factors that each ensure a role of K in invasion speed, while giving less importance to the pioneers at the border.
Two factors, the Allee effect and demographic stochasticity, make small edge populations slower to grow or less likely to survive. These two factors are studied theoretically, and to make their claims stronger, the authors stack the deck against K. When generalizing equations or simulations beyond the null case, it is easy to obtain functional forms where the parameter K does not only play the role of equilibrium carrying capacity, but also affects dynamical properties such as the maximum or mean growth rate. In that case, it can trivially change the propagation speed, without it meaning anything about the role of established populations behind the front. Haond et al [2] avoid this pitfall by disentangling these effects, at the cost of slightly more peculiar expressions, and show that varying essentially nothing but the carrying capacity can still impact the speed of the invasion front.
The third factor, density-dependent dispersal, makes small populations less prone to disperse. It is well established empirically and theoretically that various biological mechanisms, from collective organization to behavioral switches, can prompt organisms in denser populations to disperse more, e.g. in such a way as to escape competition [5]. The authors demonstrate how this effect induces a link between carrying capacity and invasion speed, both theoretically and in a dispersal experiment on the parasitoid wasp, Trichogramma chilonis.
Overall, this study carries a simple and clear message, supported by valuable contributions from different angles. Although some sections are clearly written for the theoretical ecology crowd, this article has something for everyone, from the stray physicist to the open-minded manager. The collaboration between theoreticians and experimentalists, while not central, is worthy of note. Because the narrative of this study is the variety of mechanisms that can lead to the same qualitative effect, the inclusion of various approaches is not a gimmick, but helps drive home its main message. The work is fairly self-contained, although one could always wish for further developments, especially in the direction of more quantitative testing of these mechanisms.
In conclusion, Haond et al [2] effectively convey the widely relevant message that, for some species, invading is not just about the destination, it is about the many offspring one makes along the way.
References
[1] Levins, R., & Culver, D. (1971). Regional Coexistence of Species and Competition between Rare Species. Proceedings of the National Academy of Sciences, 68(6), 1246–1248. doi: 10.1073/pnas.68.6.1246
[2] Haond, M., Morel-Journel, T., Lombaert, E., Vercken, E., Mailleret, L., & Roques, L. (2018). When higher carrying capacities lead to faster propagation. BioRxiv, 307322. doi: 10.1101/307322
[3] Crooks, E. C. M., Dancer, E. N., Hilhorst, D., Mimura, M., & Ninomiya, H. (2004). Spatial segregation limit of a competition-diffusion system with Dirichlet boundary conditions. Nonlinear Analysis: Real World Applications, 5(4), 645–665. doi: 10.1016/j.nonrwa.2004.01.004
[4] Shigesada, N., & Kawasaki, K. (1997). Biological Invasions: Theory and Practice. Oxford University Press, UK.
[5] Matthysen, E. (2005). Density-dependent dispersal in birds and mammals. Ecography, 28(3), 403–416. doi: 10.1111/j.0906-7590.2005.04073.x
Reviews: 2
In defense of the original Type I functional response: The frequency and population-dynamic effects of feeding on multiple prey at a time
Revising behavioural assumptions leads to a new appreciation of an old functional response model
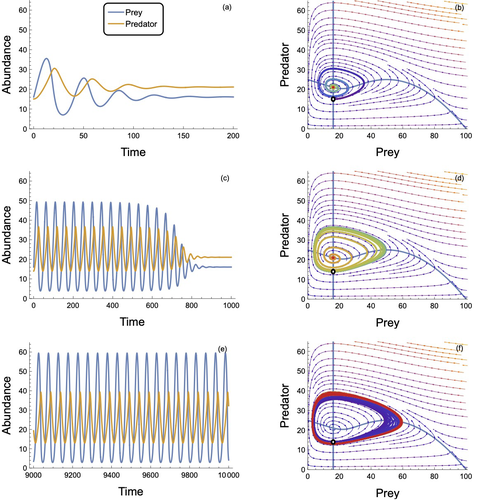
Recommended by Frédéric Barraquand based on reviews by Matthieu Barbier and Wojciech UszkoThe functional response, describing the relation between predator intake rate and prey density, is a pivotal concept to understand foraging behaviour and its consequences for community dynamics. Holling (1959a) introduced three types of functional responses according to their shapes, labelled I, II and III. The type II, also known as the disc equation (Holling 1959b), has become popular among empiricists and theoreticians alike, due to its ability to describe predator intake saturation. The type III is often used to represent predator switching to other prey species when main prey density is low.
Although theoretical works identify the linear functional response used in Lotka-Volterra models as a type I, Holling (1959a)’s type I model actually envisioned that at some threshold prey density, the linear increase in predator intake with prey density would give way to an upper predator intake limit, so that Holling’s type I has a rectilinear shape, with an angle joining straight lines. Ecology students can actually see this rectilinear shape reproduced in some texbooks, although not in textbook dynamical models, as they usually transition from Lotka-Volterra models to models with type II response.
To many, the rectilinear shape of the original type I looks like a historical curiosity: the type II functional response accounts for intake rate saturation with a more convenient smooth function.
Novak et al. (2025) turn this preconception on its head by first pedagogically showing that Holling’s original type I model can be obtained as a limit case of a variant of the celebrated type II model. The derivation follows up earlier work by Sjöberg (1980), which might be unfamiliar to readers outside aquatic ecology. The often untold assumption of the type II functional response model is that searching and handling prey are two exclusive behavioural processes, with predators that can only handle one prey item at a time. Allowing for several prey items to be handled at once while searching, until the predator reaches n prey items, the original type I functional response emerges as a limit case of the « multiprey » functional response as n goes to infinity. Interestingly, the multiprey response looks a lot like the original type I for large yet doable n.
Novak et al. (2025) then proceed to look for the prevalence of such multiprey functional response shapes in a large database of functional responses (Uiterwaal et al. 2022). Combining linear type I and multiprey models (the asymptote may not always be visible), they find support for this revised type I hypothesis in about one-third of the cases. Although the type II and III models are still well supported by data, the results do suggest that linearity at low prey density may well be more frequent than one thinks. They complement this analysis by showing that larger predators relative to their prey tend to have larger n in the multiprey response. It is consistent with the hypothesis that the bigger you are relative to your prey, the more prey items you can handle at once.
Finally, Novak et al. (2025) investigate the consequences of the multiprey model for community dynamics. They find overall a richer dynamical behaviour than the Lotka-Volterra type I and common parameterizations of the type II, suggesting that observed linearity in some range of prey density does not necessarily translate in simpler dynamical behaviour.
Novak et al. (2025) provide here a convincing and pedagogical study showing how seemingly benign behavioural assumptions can in fact profoundly alter the perceived relevance of community dynamics models. As they conclude, their analyses have lessons for future empirical functional response work, which should not necessarily dismiss the type I model and consider perhaps variants to the classical type II and III, as well as for future theoretical analyses, which could generalize this model to multiple prey species, or relax other behavioural assumptions.
References
Holling, C. S. (1959a). The components of predation as revealed by a study of small-mammal predation of the European Pine Sawfly. The Canadian Entomologist, 91(5), 293-320. https://doi.org/10.4039/Ent91293-5
Holling, C. S. (1959b). Some characteristics of simple types of predation and parasitism. The Canadian Entomologist, 91(7), 385-398. https://doi.org/10.4039/Ent91385-7
Novak, M., Coblentz, K. E., & DeLong, J. P (2025). In defense of the original Type I functional response: The frequency and population-dynamic effects of feeding on multiple prey at a time. bioRxiv, ver.4 peer-reviewed and recommended by PCI Ecology https://doi.org/10.1101/2024.05.14.594210
Sjöberg, S. (1980). Zooplankton feeding and queueing theory. Ecological Modelling, 10(3-4), 215-225. https://doi.org/10.1016/0304-3800(80)90060-5
Uiterwaal, S. F., Lagerstrom, I. T., Lyon, S. R., & DeLong, J. P. (2022). FoRAGE database: A compilation of functional responses for consumers and parasitoids. Ecology, 103(7), e3706. https://doi.org/10.1002/ecy.3706
Data-based, synthesis-driven: setting the agenda for computational ecology
Some thoughts on computational ecology from people who I’m sure use different passwords for each of their accounts
Recommended by Phillip P.A. Staniczenko based on reviews by Matthieu Barbier and 1 anonymous reviewerAre you an ecologist who uses a computer or know someone that does? Even if your research doesn’t rely heavily on advanced computational techniques, it likely hasn’t escaped your attention that computers are increasingly being used to analyse field data and make predictions about the consequences of environmental change. So before artificial intelligence and robots take over from scientists, now is great time to read about how experts think computers could make your life easier and lead to innovations in ecological research. In “Data-based, synthesis-driven: setting the agenda for computational ecology”, Poisot and colleagues [1] provide a brief history of computational ecology and offer their thoughts on how computational thinking can help to bridge different types of ecological knowledge. In this wide-ranging article, the authors share practical strategies for realising three main goals: (i) tighter integration of data and models to make predictions that motivate action by practitioners and policy-makers; (ii) closer interaction between data-collectors and data-users; and (iii) enthusiasm and aptitude for computational techniques in future generations of ecologists. The key, Poisot and colleagues argue, is for ecologists to “engage in meaningful dialogue across disciplines, and recognize the currencies of their collaborations.” Yes, this is easier said than done. However, the journey is much easier with a guide and when everyone involved serves to benefit not only from the eventual outcome, but also the process.
References
[1] Poisot, T., Labrie, R., Larson, E., & Rahlin, A. (2018). Data-based, synthesis-driven: setting the agenda for computational ecology. BioRxiv, 150128, ver. 4 recommended and peer-reviewed by PCI Ecology. doi: 10.1101/150128