
When the dispersal of the many outruns the dispersal of the few
 based on reviews by Yuval Zelnik and 1 anonymous reviewer
based on reviews by Yuval Zelnik and 1 anonymous reviewer
When higher carrying capacities lead to faster propagation
Abstract
Recommendation: posted 11 September 2018, validated 20 September 2018
Barbier, M. (2018) When the dispersal of the many outruns the dispersal of the few. Peer Community in Ecology, 100004. https://doi.org/10.24072/pci.ecology.100004
Recommendation
Are biological invasions driven by a few pioneers, running ahead of their conspecifics? Or are these pioneers constantly being caught up by, and folded into, the larger flux of propagules from the established populations behind them?
In ecology and beyond, these two scenarios are known as "pulled" and "pushed" fronts, and they come with different expectations. In a pushed front, invasion speed is not just a matter of how good individuals are at dispersing and settling new locations. It becomes a collective, density-dependent property of population fluxes. And in particular, it can depend on the equilibrium abundance of the established populations inside the range, i.e. the species’ carrying capacity K, factoring in its abiotic environment and biotic interactions.
This realization is especially important because it can flip around our expectations about which species expand fast, and how to manage them. We tend to think of initial colonization and long-term abundance as two independent axes of variation among species or indeed as two ends of a spectrum, in the classic competition-colonization tradeoff [1]. When both play into invasion speed, good dispersers might not outrun good competitors. This is useful knowledge, whether we want to contain an invasion or secure a reintroduction.
In their study "When higher carrying capacities lead to faster propagation", Haond et al [2] combine mathematical analysis, Individual-Based simulations and experiments to show that various mechanisms can cause pushed fronts, whose speed increases with the carrying capacity K of the species. Rather than focus on one particular angle, the authors endeavor to demonstrate that this qualitative effect appears again and again in a variety of settings.
It is perhaps surprising that this notable and general connection between K and invasion speed has managed to garner so little fame in ecology. A large fraction of the literature employs the venerable Fisher-KPP reaction-diffusion model, which combines local logistic growth with linear diffusion in space. This model has prompted both considerable mathematical developments [3] and many applications to modelling real invasions [4]. But it only allows pulled fronts, driven by the small populations at the edge of a species range, with a speed that depends only on their initial growth rate r.
This classic setup is, however, singular in many ways. Haond et al [2] use it as a null model, and introduce three mechanisms or factors that each ensure a role of K in invasion speed, while giving less importance to the pioneers at the border.
Two factors, the Allee effect and demographic stochasticity, make small edge populations slower to grow or less likely to survive. These two factors are studied theoretically, and to make their claims stronger, the authors stack the deck against K. When generalizing equations or simulations beyond the null case, it is easy to obtain functional forms where the parameter K does not only play the role of equilibrium carrying capacity, but also affects dynamical properties such as the maximum or mean growth rate. In that case, it can trivially change the propagation speed, without it meaning anything about the role of established populations behind the front. Haond et al [2] avoid this pitfall by disentangling these effects, at the cost of slightly more peculiar expressions, and show that varying essentially nothing but the carrying capacity can still impact the speed of the invasion front.
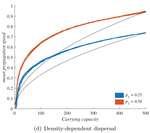
The third factor, density-dependent dispersal, makes small populations less prone to disperse. It is well established empirically and theoretically that various biological mechanisms, from collective organization to behavioral switches, can prompt organisms in denser populations to disperse more, e.g. in such a way as to escape competition [5]. The authors demonstrate how this effect induces a link between carrying capacity and invasion speed, both theoretically and in a dispersal experiment on the parasitoid wasp, Trichogramma chilonis.
Overall, this study carries a simple and clear message, supported by valuable contributions from different angles. Although some sections are clearly written for the theoretical ecology crowd, this article has something for everyone, from the stray physicist to the open-minded manager. The collaboration between theoreticians and experimentalists, while not central, is worthy of note. Because the narrative of this study is the variety of mechanisms that can lead to the same qualitative effect, the inclusion of various approaches is not a gimmick, but helps drive home its main message. The work is fairly self-contained, although one could always wish for further developments, especially in the direction of more quantitative testing of these mechanisms.
In conclusion, Haond et al [2] effectively convey the widely relevant message that, for some species, invading is not just about the destination, it is about the many offspring one makes along the way.
References
[1] Levins, R., & Culver, D. (1971). Regional Coexistence of Species and Competition between Rare Species. Proceedings of the National Academy of Sciences, 68(6), 1246–1248. doi: 10.1073/pnas.68.6.1246
[2] Haond, M., Morel-Journel, T., Lombaert, E., Vercken, E., Mailleret, L., & Roques, L. (2018). When higher carrying capacities lead to faster propagation. BioRxiv, 307322. doi: 10.1101/307322
[3] Crooks, E. C. M., Dancer, E. N., Hilhorst, D., Mimura, M., & Ninomiya, H. (2004). Spatial segregation limit of a competition-diffusion system with Dirichlet boundary conditions. Nonlinear Analysis: Real World Applications, 5(4), 645–665. doi: 10.1016/j.nonrwa.2004.01.004
[4] Shigesada, N., & Kawasaki, K. (1997). Biological Invasions: Theory and Practice. Oxford University Press, UK.
[5] Matthysen, E. (2005). Density-dependent dispersal in birds and mammals. Ecography, 28(3), 403–416. doi: 10.1111/j.0906-7590.2005.04073.x
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
Reviewed by Yuval Zelnik, 05 Sep 2018
I was quite happy with the changes the authors have made, which I think make the paper clearer and more approachable. I am now happy to recommend this paper.
As a small note, in the discussion both the second and third paragraphs start with "Positive density-dependent dispersal..." which I assume was not intentional, and perhaps should be changed.
https://doi.org/10.24072/pci.ecology.100004.rev21Evaluation round #1
DOI or URL of the preprint: https://doi.org/10.1101/307322
Version of the preprint: 1
Author's Reply, 24 Aug 2018
Decision by Matthieu Barbier , posted 24 Aug 2018
, posted 24 Aug 2018
Dear Authors,
First of all, I must give you my sincere apologies for the unpleasant lateness of this reply, as the process of obtaining reviews was unfortunately a rather bumpy one. I will make sure that no such delays occur for the rest of the recommendation process.
Both reviewers and myself have found significant interest in your work, and this manuscript will certainly be worthy of recommendation.
I particularly applaud the joint use of theory and experiments, which is far too rare in our fields.
The reviewers have however noted a list of concerns which mandate some clarifications and minor revisions before recommendation. I will add some of my own comments:
1) In particular, I would also like clearer motivations concerning your competition step and equation (4). This choice for competition may be responsible for the quick saturation with K, and this effect (that the stochastic IBM sees faster saturation with K than the deterministic equations) might go against the message that demographic stochasticity could increase the role of K, thankfully illustrated in Fig 4a at least.
There is no doubt that, for any reasonable continuous equation, one can construct an IBM that will reproduce its results exactly, so I suppose that the IBM came first (or was modelled after the experiments) and equation (4) strives to reproduce its results?
Or are you trying to make the strongest possible case by ensuring that, even when limiting the influence of K as much as possible (giving it no role before N reaches it in the IBM, and removing it from the max growth rate in (4) ), it still plays a role? The motivation for these choices should made be clearer.
2) As it turns out, the two reviewers and myself unfortunately share a theoretical bent, but the experimental and statistical aspects appear to me to be sound. However, I think the paragraph on the experimental results could be put in more relief (perhaps given its own section).
First, it is not so clear in the text why you would interpret this result as density-dependent dispersal, rather than any of your other mechanisms (hence putting it together with density-dependent dispersal results is not so obvious)
Second, you could perhaps present the qualitative results first, so as to limit the necessity to go back to the Methods to interpret what is said. For the less statistically minded, as I am, describing the effect of carrying capacity as an interaction between generation and modality is a counter-intuitive phrasing of a very intuitive idea.
Sincerely,
Matthieu Barbier
Reviewed by Yuval Zelnik, 05 Jun 2018
This manuscript attempts to disentangle different mechanisms and processes that effect front propagation (e.g. species invasion), and in particular focuses on the role of carrying capacity in this context. The authors use three distinct methodologies, the more analytically tractable Reaction-Diffusion (RD) approach, the more numerical Individual Based Modeling (IBM), and the more grounded in reality microcosms experiment. They use a combination of these three approaches to arrive at a more general conclusion of how a species carrying capacity affects the speed in which it invades a region devoid of this species.
Overall the paper is well written, gives a good introduction to the topic, uses a sound methodology and attention to details, and does a good job of using the different methodologies available to reach an understanding of the question it raises. Since this proposed question on propagation speed is both interesting from a theoretical perspective and important from a practical one of species invasions, I find it to be a useful and enlightening study.
I have a few comments and concerns of varying importance, which I give below.
1) In the RD case (e.g. eq. 1) I wonder if there isn't a problem with the front speed being set by the low populations since with the assumption of diffusion the tail is infinitely long (i.e. no finite support)?
2) I think it is worth noting that equations 4 and 5 are not consistent in their units. This should probably be mentioned or amended.
3) The competition step for the IBM is quite strange. Is it perhaps the reason why the front is very sharp (fig. 2)? From a first glance, it appears that low populations are "safe" while beyond K they can collapse from this step. I realize that the reproduction step is the main cause of demographics and thus local population collapse, but I wonder what would happen to the front speed if the assumptions of the competition is changed. In particular, since the focus of this modeling approach is exactly to look at the importance of the carrying capacity, I think it would be good to make sure that there's nothing particular to this choice of implementation. Or perhaps there is a clear reason why this choice is sound from a mechanistic perspective?
4) Indeed the eq. 4 looks like a better "fit", but why? That is, it would be helpful to give intuition on what "went wrong" when constructing the model in eq. 3. Also where does the extra speed of IBMs come from?
5) Would it not be possible to develop the IBM into a continuous form in the density dependence case? This should lead to a better explanation of the discrepancy between IBMs and RD in Fig. 4d
6) Except for the third part of the discussion, which I find quite interesting, I find the discussion lacking as it mostly summarizes the results. I think it would be useful to add a discussion on the reasons for the different results shown, and to consider how one might distinguish between different scenarios where high K leads to faster speeds.
7) Also, I feel that you could use the discussion to better give context on what your results mean from a practical perspective (i.e., what does this mean to conservation?). While I assume this paper is geared more to a theoretical crowd, some thoughts on implications would probably be useful to many people.
8) In the SI, I am not sure if there is a clear added value in the content on the weak Allee effect, but if it is already there, why not compare the IBM results in Fig.3 (of the SI) to the theoretical ones mentioned earlier?
https://doi.org/10.24072/pci.ecology.100007.rev11









