Are biological invasions driven by a few pioneers, running ahead of their conspecifics? Or are these pioneers constantly being caught up by, and folded into, the larger flux of propagules from the established populations behind them?
In ecology and beyond, these two scenarios are known as "pulled" and "pushed" fronts, and they come with different expectations. In a pushed front, invasion speed is not just a matter of how good individuals are at dispersing and settling new locations. It becomes a collective, density-dependent property of population fluxes. And in particular, it can depend on the equilibrium abundance of the established populations inside the range, i.e. the species’ carrying capacity K, factoring in its abiotic environment and biotic interactions.
This realization is especially important because it can flip around our expectations about which species expand fast, and how to manage them. We tend to think of initial colonization and long-term abundance as two independent axes of variation among species or indeed as two ends of a spectrum, in the classic competition-colonization tradeoff [1]. When both play into invasion speed, good dispersers might not outrun good competitors. This is useful knowledge, whether we want to contain an invasion or secure a reintroduction.
In their study "When higher carrying capacities lead to faster propagation", Haond et al [2] combine mathematical analysis, Individual-Based simulations and experiments to show that various mechanisms can cause pushed fronts, whose speed increases with the carrying capacity K of the species. Rather than focus on one particular angle, the authors endeavor to demonstrate that this qualitative effect appears again and again in a variety of settings.
It is perhaps surprising that this notable and general connection between K and invasion speed has managed to garner so little fame in ecology. A large fraction of the literature employs the venerable Fisher-KPP reaction-diffusion model, which combines local logistic growth with linear diffusion in space. This model has prompted both considerable mathematical developments [3] and many applications to modelling real invasions [4]. But it only allows pulled fronts, driven by the small populations at the edge of a species range, with a speed that depends only on their initial growth rate r.
This classic setup is, however, singular in many ways. Haond et al [2] use it as a null model, and introduce three mechanisms or factors that each ensure a role of K in invasion speed, while giving less importance to the pioneers at the border.
Two factors, the Allee effect and demographic stochasticity, make small edge populations slower to grow or less likely to survive. These two factors are studied theoretically, and to make their claims stronger, the authors stack the deck against K. When generalizing equations or simulations beyond the null case, it is easy to obtain functional forms where the parameter K does not only play the role of equilibrium carrying capacity, but also affects dynamical properties such as the maximum or mean growth rate. In that case, it can trivially change the propagation speed, without it meaning anything about the role of established populations behind the front. Haond et al [2] avoid this pitfall by disentangling these effects, at the cost of slightly more peculiar expressions, and show that varying essentially nothing but the carrying capacity can still impact the speed of the invasion front.
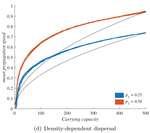
The third factor, density-dependent dispersal, makes small populations less prone to disperse. It is well established empirically and theoretically that various biological mechanisms, from collective organization to behavioral switches, can prompt organisms in denser populations to disperse more, e.g. in such a way as to escape competition [5]. The authors demonstrate how this effect induces a link between carrying capacity and invasion speed, both theoretically and in a dispersal experiment on the parasitoid wasp, Trichogramma chilonis.
Overall, this study carries a simple and clear message, supported by valuable contributions from different angles. Although some sections are clearly written for the theoretical ecology crowd, this article has something for everyone, from the stray physicist to the open-minded manager. The collaboration between theoreticians and experimentalists, while not central, is worthy of note. Because the narrative of this study is the variety of mechanisms that can lead to the same qualitative effect, the inclusion of various approaches is not a gimmick, but helps drive home its main message. The work is fairly self-contained, although one could always wish for further developments, especially in the direction of more quantitative testing of these mechanisms.
In conclusion, Haond et al [2] effectively convey the widely relevant message that, for some species, invading is not just about the destination, it is about the many offspring one makes along the way.

References

[1] Levins, R., & Culver, D. (1971). Regional Coexistence of Species and Competition between Rare Species. Proceedings of the National Academy of Sciences, 68(6), 1246–1248. doi: 10.1073/pnas.68.6.1246
[2] Haond, M., Morel-Journel, T., Lombaert, E., Vercken, E., Mailleret, L., & Roques, L. (2018). When higher carrying capacities lead to faster propagation. BioRxiv, 307322. doi: 10.1101/307322
[3] Crooks, E. C. M., Dancer, E. N., Hilhorst, D., Mimura, M., & Ninomiya, H. (2004). Spatial segregation limit of a competition-diffusion system with Dirichlet boundary conditions. Nonlinear Analysis: Real World Applications, 5(4), 645–665. doi: 10.1016/j.nonrwa.2004.01.004
[4] Shigesada, N., & Kawasaki, K. (1997). Biological Invasions: Theory and Practice. Oxford University Press, UK.
[5] Matthysen, E. (2005). Density-dependent dispersal in birds and mammals. Ecography, 28(3), 403–416. doi: 10.1111/j.0906-7590.2005.04073.x