
MUNOZ François
- Laboratoire Interdisciplinaire de Physique, Université Grenoble Alpes, Grenoble, France
- Biodiversity, Biogeography, Botany, Coexistence, Community ecology, Conservation biology, Eco-evolutionary dynamics, Ecological successions, Evolutionary ecology, Interaction networks, Landscape ecology, Macroecology, Ontogeny, Phylogeny & Phylogeography, Population ecology, Spatial ecology, Metacommunities & Metapopulations, Species distributions, Statistical ecology, Terrestrial ecology, Theoretical ecology, Tropical ecology
- recommender
Recommendations: 7
Reviews: 0
Recommendations: 7
On the quest for novelty in ecology
From Paradigm to Publication: What Does the Pursuit of Novelty Reveal in Ecology?
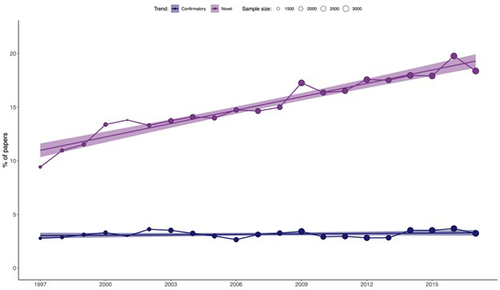
Recommended by François Munoz based on reviews by Francois Massol, Matthias Grenié and 1 anonymous reviewerIn this study, Ottaviani et al. (2025) examined the variation in the use of terms related to "novelty" in 52,236 abstracts published between 1997 and 2017 across 17 ecological journals. They also analyzed the change in the frequency of terms related to "confirmatory" results. Their findings revealed a clear and consistent increase in the use of "novelty" terms, while the frequency of "confirmatory" terms remained relatively stable. This trend was observed across all the ecological journals, with the exception of Austral Ecology. Furthermore, the greater use of "novelty" terms was correlated with higher citation counts and publication in journals with higher impact factors. These findings should prompt further reflection on our research practices and may be connected to ongoing discussions in the philosophy of science.
Thomas S. Kuhn's seminal work, The Structure of Scientific Revolutions (1962), challenged traditional views of scientific progress. Central to Kuhn's argument is the idea that science progresses through periods of adherence to a dominant "paradigm"—a framework that provides scientists with puzzles to solve and the tools to solve them. A scientific crisis arises when the paradigm fails to address emerging anomalies, leading to the replacement of the old paradigm with a new one, a process Kuhn calls a "scientific revolution." Kuhn's perspective stands in stark contrast to previous views, which held that science progresses through the steady accumulation of truths or the gradual refinement of theories, often guided by the scientific method. One might wonder if the growing emphasis on "novelty" in ecological research mirrors the idea that theories are gradually refined until an exceptional discovery sparks a paradigm shift. In ecology, such a shift could be seen in the transition from niche-based theories of biodiversity dynamics (1960s-2000) to the radical neutral theory (Hubbell, 2001), which posits that diverse ecosystems can exist without niche differences. This paradigm was initially met with fierce opposition but eventually led to more integrative theories, recognizing the combined influence of both niche-based and neutral processes (Gravel et al., 2006, among others).
What, then, is the current paradigm in ecology? Kuhn's theory of scientific progress suggests alternating periods of "normal" and "revolutionary" science. Normal science is characterized by cumulative puzzle-solving within established frameworks, while revolutionary science involves major shifts that can invalidate previous knowledge, a phenomenon Kuhn terms "Kuhn-loss." Kuhn rejected both the traditional and Popperian views on scientific revolutions. He argued that normal science depends on a shared commitment to certain beliefs, values, methods, and even metaphysical assumptions, which he referred to as a "disciplinary matrix" or "paradigm." This collective commitment is essential for scientific progress and must be instilled during the training of scientists. Kuhn's emphasis on the conservative nature of normal science contrasts with the heroic idea of continuous innovation and Popper's view of scientists constantly seeking to falsify theories. However, contemporary ecological research often follows the hypothetico-deductive approach championed by Popper. In light of these contrasting views, one might ask: What is the status of "novelty" in modern ecology? Is it contributing to the gradual solving of scientific puzzles, or is it focused on refuting hypotheses? Should "novelty" and "confirmatory" research be seen as opposites, or should both contribute to the advancement of science? Finally, is the increasing use of "novelty" terms a precursor to a scientific revolution, as Kuhn defined it, or merely a semantic trend driven by editorial policies aimed at attracting readers rather than contributing to real scientific progress?
In conclusion, Ottaviani's study provides compelling evidence of the growing use of "novelty" terms in ecological journals, but it remains unclear whether this trend signals the onset of a Kuhnian "scientific revolution." This work should spark further discussion on the nature of current research practices, which may either facilitate or hinder the emergence of new paradigms.
References
Gravel, D., Canham, C. D., Beaudet, M., & Messier, C. (2006). Reconciling niche and neutrality: the continuum hypothesis. Ecology letters, 9(4), 399-409. https://doi.org/10.1111/j.1461-0248.2006.00884.x
Hubbell, S. P. (2001). The Unified Neutral Theory of Biodiversity and Biogeography, vol.1, Princeton and Oxford: Princeton University Press.
Kuhn, T. S. (1962). The structure of scientific revolutions. International Encyclopedia of Unified Science, vol.2, 1962.
Ottaviani, G., Martinez, A., Petit Bon, M., Mammola, S. (2025). On the quest for novelty in ecology. bioRxiv, ver.4 peer-reviewed and recommended by PCI Ecology. https://doi.org/10.1101/2023.02.27.530333
Predicting species distributions in the open ocean with convolutional neural networks
The potential of Convolutional Neural Networks for modeling species distributions
Recommended by François Munoz based on reviews by Jean-Olivier Irisson, Sakina-Dorothee Ayata and 1 anonymous reviewerMorand et al. (2024) designed convolutional neural networks to predict the occurrences of 38 marine animals worldwide. The environmental predictors were sea surface temperature, chlorophyll concentration, salinity and fifteen others. The time of some of the predictors was chosen to be as close as possible to the time of the observed occurrence.
This approach has previously only been applied to the analysis of the distribution of terrestrial plant species (Botella et al. 2018, Deneu et al. 2021), so the application here to very different marine ecosystems and organisms is a novelty worth highlighting and discussing.
A very interesting feature of PCI Ecology is that reviews are provided with the final manuscript and the present recommendation text.
In the case of the Morand et al. article, the reviewers provided very detailed and insightful comments that deserve to be published and read alongside the article.
The reviewers' comments question the ecological significance and implications of choosing fine temporal and spatial scales in CNN distribution modelling in order to obtain species distribution modelling (SDM).
The main question debated during the review process was whether the CNN modeling approach used here can be defined as a kind of niche modeling.
The fact is that most of the organisms studied here are mobile, and the authors have taken into account precise environmental information at dates close to those of species appearance (for example, "Temperature and chlorophyll values were also included 15 and 5 days before the occurrences"). In doing so, they took into account the fine spatial and temporal scales of species occurrences and environmental conditions, which can be influenced by both environmental preferences and the movement behaviors of individuals. The question then arises: does this approach really represent the ecological niches of the marine organisms selected? Given that most selected organisms may have specific seasonal movement dynamics, the CNN model also learns the individual movement behaviors of organisms over seasons and years. The ecological niche is a broader concept that takes into account all the environmental conditions that enable species to persist over the course of their lives and over generations. This differs from the case of sessile land plants, which must respond to the environmental context only at the points of appearance.
This is not a shortcoming of the methodology proposed here but rather an interesting conceptual issue to be considered and discussed. Modelling the occurrence of individuals at a given time and position can characterize not only the species' niche but also the dynamics of organisms' temporal movements. As a result, the model predicts the position of individuals at a given time, while the niche should also represent the role of environmental conditions faced by individuals at other times in their lives.
A relevant perspective would then be to analyze whether and how the neural network can help disentangle the ranges of environmental conditions defining the niche from those influencing the movement dynamics of individuals.
Another interesting point is that the CNN model is used here as a multi-species classifier, meaning that it provides the ranked probability that a given observation corresponds to one of the 38 species considered in the study, depending on the environmental conditions at the location and time of the observation. In other words, the model provides the relative chance of choosing each of the 38 species at a given time and place. Imagine that you are only studying two species that have exactly the same niche, a standard SDM approach should provide a high probability of occurrence close to 1 in localities where environmental conditions are very and equally suited to both species, while the CNN classifier would provide a value close to 0.5 for both species, meaning that we have an equal chance of choosing one or the other. Consequently, the fact that the probability given by the classifier is higher for a species at a given point than at another point does not (necessarily) mean that the first point presents better environmental conditions for that species but rather that we are more likely to choose it over one of the other species at this point than at another. In fact, the classification task also reflects whether the other 37 species are more or less likely to be found at each point. The classifier, therefore, does not provide the relative probability of occurrence of a species in space but rather a relative chance of finding it instead of one of the other 37 species at each point of space and time.
It is important that an ecologist designing a multi-species classifier for species distribution modelling is well aware of this point and does not interpret the variation of probabilities for a species in space as an indication of more or less suitable habitat for that specific species. On the other hand, predicting the relative probabilities of finding species to a given point at a given time gives an indication of the dynamics of their local co-occurrence. In this respect, the CNN approach is closer to a joint species distribution model (jSDM). As Ovaskainen et al. (2017) mention, "By simultaneously drawing on the information from multiple species, these (jSDM) models allow one to seek community-level patterns in how species respond to their environment". Let's return to the two species example we used above. The fact that the probabilities are 0.5 for both species actually suggests that both species can coexist at the same abundance at this location. In this respect, the CNN multi-species classifier offers promising prospects for the prediction of assemblages and habitats thanks to the relative importance of the most characteristic/dominant species from a species pool. The species pool comprises all classified species and must be sufficiently representative of the ecological diversity of species niches in the area.
Finally, CNN-based species distribution modelling is a powerful and promising tool for studying the distributions of multi-species assemblages as a function of local environmental features but also of the spatial heterogeneity of each feature around the observation point in space and time (Deneu et al. 2021). It allows acknowledging the complex effects of environmental predictors and the roles of their spatial and temporal heterogeneity through the convolution operations performed in the neural network. As more and more computationally intensive tools become available, and as more and more environmental data becomes available at finer and finer temporal and spatial scales, the CNN approach is likely to be increasingly used to study biodiversity patterns across spatial and temporal scales.
References
Botella, C., Joly, A., Bonnet, P., Monestiez, P., and Munoz, F. (2018). Species distribution modeling based on the automated identification of citizen observations. Applications in Plant Sciences, 6(2), e1029. https://doi.org/10.1002/aps3.1029
Deneu, B., Servajean, M., Bonnet, P., Botella, C., Munoz, F., and Joly, A. (2021). Convolutional neural networks improve species distribution modelling by capturing the spatial structure of the environment. PLoS Computational Biology, 17(4), e1008856. https://doi.org/10.1371/journal.pcbi.1008856
Morand, G., Joly, A., Rouyer, T., Lorieul, T., and Barde, J. (2024) Predicting species distributions in the open ocean with convolutional neural networks. bioRxiv, ver.3 peer-reviewed and recommended by PCI Ecology https://doi.org/10.1101/2023.08.11.551418
Ovaskainen, O., Tikhonov, G., Norberg, A., Guillaume Blanchet, F., Duan, L., Dunson, D., ... and Abrego, N. (2017). How to make more out of community data? A conceptual framework and its implementation as models and software. Ecology letters, 20(5), 561-576. https://doi.org/10.1111/ele.12757
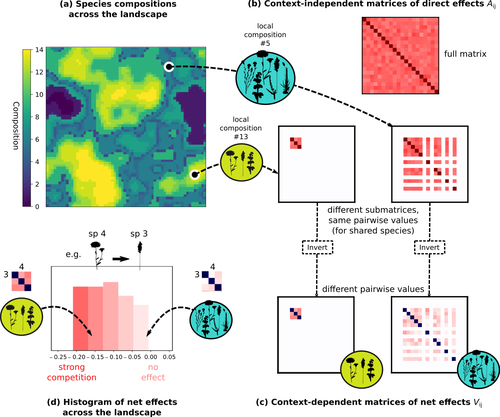
Getting More by Asking for Less: Linking Species Interactions to Species Co-Distributions in Metacommunities
Beyond pairwise species interactions: coarser inference of their joined effects is more relevant
Recommended by François Munoz based on reviews by Frederik De Laender, Hao Ran Lai and Malyon BimlerBarbier et al. (2024) investigated the dynamics of species abundances depending on their ecological niche (abiotic component) and on (numerous) competitive interactions. In line with previous evidence and expectations (Barbier et al. 2018), the authors show that it is possible to robustly infer the mean and variance of interaction coefficients from species co-distributions, while it is not possible to infer the individual coefficient values.
The authors devised a simulation framework representing multispecies dynamics in an heterogeneous environmental context (2D grid landscape). They used a Lotka-Volterra framework involving pairwise interaction coefficients and species-specific carrying capacities. These capacities depend on how well the species niche matches the local environmental conditions, through a Gaussian function of the distance of the species niche centers to the local environmental values.
They considered two contrasted scenarios denoted as « Environmental tracking » and « Dispersal limited ». In the latter case, species are initially seeded over the environmental grid and cannot disperse to other cells, while in the former case they can disperse and possibly be more performant in other cells.
The direct effects of species on one another are encoded in an interaction matrix A, and the authors further considered net interactions depending on the inverse of the matrix of direct interactions (Zelnik et al., 2024). The net effects are context-dependent, i.e., it involves the environment-dependent biotic capacities, even through the interaction terms can be defined between species as independent from local environment.
The results presented here underline that the outcome of many individual competitive interactions can only be understood in terms of macroscopic properties. In essence, the results here echoe the mean field theories that investigate the dynamics of average ecological properties instead of the microscopic components (e.g., McKane et al. 2000). In a philosophical perspective, community ecology has long struggled with analyzing and inferring local determinants of species coexistence from species co-occurrence patterns, so that it was claimed that no universal laws can be derived in the discipline (Lawton 1999). Using different and complementary methods and perspectives, recent research has also shown that species assembly parameter values cannot be unambiguously inferred from species co-occurrences only, even in simple designs where an equilibrium can be reached (Poggiato et al. 2021). Although the roles of high-order competitive interactions and intransivity can lead to species coexistence, the simple view of a single loop of competitive interactions is easily challenged when further interactions and complexity is added (Gallien et al. 2024). But should we put so much emphasis on inferring individual interaction coefficients? In a quest to understand the emerging properties of elementary processes, ecological theory could go forward with a more macroscopic analysis and understanding of species coexistence in many communities.
The authors referred several times to an interesting paper from Schaffer (1981), entitled « Ecological abstraction: the consequences of reduced dimensionality in ecological models ». It proposes that estimating individual species competition coefficients is not possible, but that competition can be assessed at the coarser level of organisation, i.e., between ecological guilds. This idea implies that the dimensionality of the competition equations should be greatly reduced to become tractable in practice. Taking together this claim with the results of the present Barbier et al. (2024) paper, it becomes clearer that the nature of competitive interactions can be addressed through « abstracted » quantities, as those of guilds or the moments of the individual competition coefficients (here the average and the standard deviation).
Therefore the scope of Barbier et al. (2024) framework goes beyond statistical issues in parameter inference, but question the way we must think and represent the numerous competitive interactions in a simplified and robust way.
References
Barbier, Matthieu, Jean-François Arnoldi, Guy Bunin, et Michel Loreau. 2018. « Generic assembly patterns in complex ecological communities ». Proceedings of the National Academy of Sciences 115 (9): 2156‑61. https://doi.org/10.1073/pnas.1710352115
Barbier, Matthieu, Guy Bunin, et Mathew A Leibold. 2024. « Getting More by Asking for Less: Linking Species Interactions to Species Co-Distributions in Metacommunities ». bioRxiv, ver. 2 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2023.06.04.543606
Gallien, Laure, Maude Charlie Cavaliere, Marie Charlotte Grange, François Munoz, et Tamara Münkemüller. 2024. « Intransitive stability collapses under the influence of dominant competitors ». The American Naturalist. https://doi.org/10.1086/730297
Lawton, J. H. 1999. « Are There General Laws in Ecology? » Oikos 84 (février):177‑92. https://doi.org/10.2307/3546712
McKane, Alan, David Alonso, et Ricard V Solé. 2000. « Mean-field stochastic theory for species-rich assembled communities ». Physical Review E 62 (6): 8466. https://doi.org/10.1103/PhysRevE.62.8466
Poggiato, Giovanni, Tamara Münkemüller, Daria Bystrova, Julyan Arbel, James S. Clark, et Wilfried Thuiller. 2021. « On the Interpretations of Joint Modeling in Community Ecology ». Trends in Ecology & Evolution. https://doi.org/10.1016/j.tree.2021.01.002
Schaffer, William M. 1981. « Ecological abstraction: the consequences of reduced dimensionality in ecological models ». Ecological monographs 51 (4): 383‑401. https://doi.org/10.2307/2937321
Zelnik, Yuval R., Nuria Galiana, Matthieu Barbier, Michel Loreau, Eric Galbraith, et Jean-François Arnoldi. 2024. « How collectively integrated are ecological communities? » Ecology Letters 27 (1): e14358. https://doi.org/10.1111/ele.14358
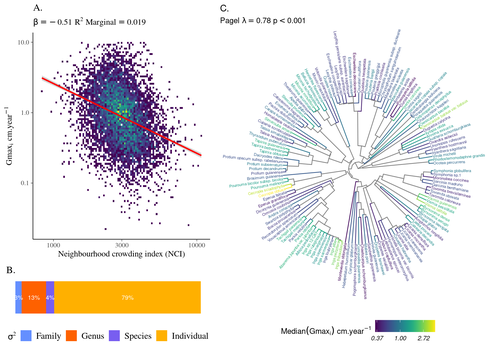
High intraspecific growth variability despite strong evolutionary heritage in a neotropical forest
Environmental and functional determinants of tree performance in a neotropical forest: the imprint of evolutionary legacy on growth strategies
Recommended by François Munoz based on reviews by David Murray-Stoker, Camille Girard and Jelena PantelThe hyperdiverse tropical forests have long fascinated ecologists because the fact that so many species persist at a low density at a local scale remains hard to explain. Both niche-based and neutral hypotheses have been tested, primarily based on analyzing the taxonomic composition of tropical forest plots (Janzen 1970; Hubbell 2001). Studies of the functional and phylogenetic structure of tropical tree communities have further aimed to better assess the importance of niche-based processes. For instance, Baraloto et al. (2012) found that co-occurring species were functionally and phylogenetically more similar in a neotropical forest, suggesting a role of environmental filtering. Likewise, Schmitt et al. (2021) found the influence of environmental filtering on the functional composition of an Indian rainforest. Yet these studies evidenced non-random trait-environment association based on the composition of assemblages only (in terms of occurrences and abundances). A major challenge remains to further address whether and how tree performance varies among species and individuals in tropical forests.
Functional traits are related to components of individual fitness (Violle et al. 2007). Recently, more and more emphasis has been put on examining the relationship between functional trait values and demographic parameters (Salguero-Gómez et al. 2018), in order to better understand how functional trait values determine species population dynamics and abundances in assemblages. Fortunel et al. (2018) found an influence of functional traits on species growth variation related to topography, and less clearly to neighborhood density (crowding). Poorter et al. (2018) observed 44% of trait variation within species in a neotropical forest. Although individual trait values would be expected to be better predictors of performance than average values measured at the species level, Poorter et al still found a poor relationship.
Schmitt et al. (2023) examined how abiotic conditions and biotic interactions (considering neighborhood density) influenced the variation of individual potential tree growth, in a tropical forest plot located in French Guiana. They also considered the link between species-averaged values of growth potential and functional traits. Schmitt et al. (2023) found substantial variation in growth potential within species, that functional traits explained 40% of the variation of species-averaged growth and, noticeably, that the taxonomic structure (used as random effect in their model) explained a third of the variation in individual growth.
Although functional traits of roots, wood and leaves could predict a significant part of species growth potential, much variability of tree growth occurred within species. Intraspecific trait variation can thus be huge in response to changing abiotic and biotic contexts across individuals. The information on phylogenetic relationships can still provide a proxy of the integrated phenotypic variation that is under selection across the phylogeny, and determine a variation in growth strategies among individuals. The similarity of the phylogenetic structure suggests a joint selection of these growth strategies and related functional traits during events of convergent evolution. Baraloto et al. (2012) already noted that phylogenetic distance can be a proxy of niche overlap in tropical tree communities. Here, Schmitt et al. further demonstrate that evolutionary heritage is significantly related to individual growth variation, and plead for better acknowledging this role in future studies.
While the role of fitness differences in tropical tree community dynamics remained to be assessed, the present study provides new evidence that individual growth does vary depending on evolutionary relationships, which can reflect the roles of selection and adaptation on growth strategies. Therefore, investigating both the influence of functional traits and phylogenetic relationships on individual performance remains a promising avenue of research, for functional and community ecology in general.
REFERENCES
Baraloto, Christopher, Olivier J. Hardy, C. E. Timothy Paine, Kyle G. Dexter, Corinne Cruaud, Luke T. Dunning, Mailyn-Adriana Gonzalez, et al. 2012. « Using functional traits and phylogenetic trees to examine the assembly of tropical tree communities ». Journal of Ecology, 100: 690‑701.
https://doi.org/10.1111/j.1365-2745.2012.01966.x
Fortunel Claire, Lasky Jesse R., Uriarte María, Valencia Renato, Wright S.Joseph, Garwood Nancy C., et Kraft Nathan J. B. 2018. « Topography and neighborhood crowding can interact to shape species growth and distribution in a diverse Amazonian forest ». Ecology, 99(10): 2272-2283. https://doi.org/10.1002/ecy.2441
Hubbell, S. P. 2001. The Unified Neutral Theory of Biodiversity and Biogeography. 1 vol. Princeton and Oxford: Princeton University Press. https://www.jstor.org/stable/j.ctt7rj8w
Janzen, Daniel H. 1970. « Herbivores and the number of tree species in tropical forests ». American Naturalist, 104(940): 501-528. https://doi.org/10.1086/282687
Poorter, Lourens, Carolina V. Castilho, Juliana Schietti, Rafael S. Oliveira, et Flávia R. C. Costa. 2018. « Can traits predict individual growth performance? A test in a hyperdiverse tropical forest ». New Phytologist, 219 (1): 109‑21. https://doi.org/10.1111/nph.15206
Salguero-Gómez, Roberto, Cyrille Violle, Olivier Gimenez, et Dylan Childs. 2018. « Delivering the promises of trait-based approaches to the needs of demographic approaches, and vice versa ». Functional Ecology, 32 (6): 1424‑35. https://doi.org/10.1111/1365-2435.13148
Schmitt, Sylvain, Valérie Raevel, Maxime Réjou‐Méchain, Narayanan Ayyappan, Natesan Balachandran, Narayanan Barathan, Gopalakrishnan Rajashekar, et François Munoz. 2021. « Canopy and understory tree guilds respond differently to the environment in an Indian rainforest ». Journal of Vegetation Science, e13075. https://doi.org/10.1111/jvs.13075
Sylvain Schmitt, Bruno Hérault, et Géraldine Derroire. 2023. « High intraspecific growth variability despite strong evolutionary heritage in a neotropical forest ». bioRxiv, 2022.07.27.501745, ver. 3 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2022.07.27.501745
Violle, C., M. L. Navas, D. Vile, E. Kazakou, C. Fortunel, I. Hummel, et E. Garnier. 2007. « Let the concept of trait be functional! » Oikos, 116(5), 882-892. https://doi.org/10.1111/j.0030-1299.2007.15559.x

Dissimilarity of species interaction networks: quantifying the effect of turnover and rewiring
How to evaluate and interpret the contribution of species turnover and interaction rewiring when comparing ecological networks?
Recommended by François Munoz based on reviews by Ignasi Bartomeus and 1 anonymous reviewerA network includes a set of vertices or nodes (e.g., species in an interaction network), and a set of edges or links (e.g., interactions between species). Whether and how networks vary in space and/or time are questions often addressed in ecological research.
Two ecological networks can differ in several extents: in that species are different in the two networks and establish new interactions (species turnover), or in that species that are present in both networks establish different interactions in the two networks (rewiring). The ecological meaning of changes in network structure is quite different according to whether species turnover or interaction rewiring plays a greater role. Therefore, much attention has been devoted in recent years on quantifying and interpreting the relative changes in network structure due to species turnover and/or rewiring.
Poisot et al. (2012) proposed to partition the global variation in structure between networks, \( \beta_{WN} \) (WN = Whole Network) into two terms: \( \beta_{OS} \) (OS = Only Shared species) and \( \beta_{ST} \) (ST = Species Turnover), such as \( \beta_{WN} = \beta_{OS} + \beta_{ST} \).
The calculation lays on enumerating the interactions between species that are common or not to two networks, as illustrated on Figure 1 for a simple case. Specifically, Poisot et al. (2012) proposed to use a Sorensen type measure of network dissimilarity, i.e., \( \beta_{WN} = \frac{a+b+c}{(2a+b+c)/2} -1=\frac{b+c}{2a+b+c} \) , where \( a \) is the number of interactions shared between the networks, while \( b \) and \( c \) are interaction numbers unique to one and the other network, respectively. \( \beta_{OS} \) is calculated based on the same formula, but only for the subnetworks including the species common to the two networks, in the form \( \beta_{OS} = \frac{b_{OS}+c_{OS}}{2a_{OS}+b_{OS}+c_{OS}} \) (e.g., Fig. 1). \( \beta_{ST} \) is deduced by subtracting \( \beta_{OS} \) from \( \beta_{WN} \) and represents in essence a "dissimilarity in interaction structure introduced by dissimilarity in species composition" (Poisot et al. 2012).
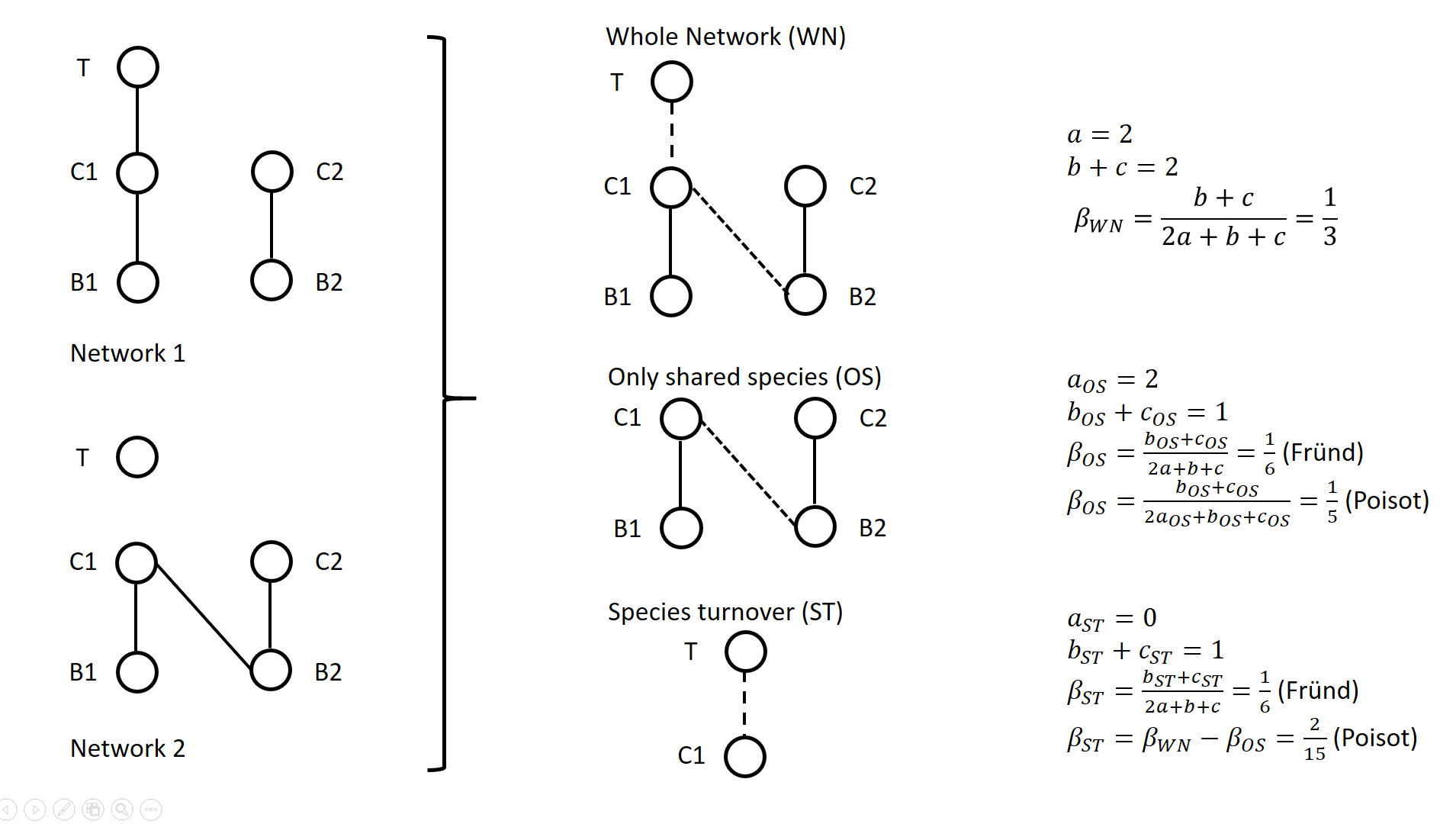
Figure 1. Ecological networks exemplified in Fründ (2021) and discussed in Poisot (2022). a is the number of shared links (continuous lines in right figures), while b+c is the number of edges unique to one or the other network (dashed lines in right figures).
Alternatively, Fründ (2021) proposed to define \( \beta_{OS} = \frac{b_{OS}+c_{OS}}{2a+b+c} \) and \( \beta_{ST} = \frac{b_{ST}+c_{ST}}{2a+b+c} \), where \( b_{ST}=b-b_{OS} \) and \( c_{ST}=c-c_{OS} \) , so that the components \( \beta_{OS} \) and \( \beta_{ST} \) have the same denominator. In this way, Fründ (2021) partitioned the count of unique \( b+c=b_{OS}+b_{ST}+c_{ST} \) interactions, so that \( \beta_{OS} \) and \( \beta_{ST} \) sums to \( \frac{b_{OS}+c_{OS}+b_{ST}+c_{ST}}{2a+b+c} = \frac{b+c}{2a+b+c} = \beta_{WN} \). Fründ (2021) advocated that this partition allows a more sensible comparison of \( \beta_{OS} \) and \( \beta_{ST} \), in terms of the number of links that contribute to each component.
For instance, let us consider the networks 1 and 2 in Figure 1 (left panel) such as \( a_{OS}=2 \) (continuous lines in right panel), \( b_{ST} + c_{ST} = 1 \) and \( b_{OS} + c_{OS} = 1 \) (dashed lines in right panel), and thereby \( a = 2 \), \( b+c=2 \), \( \beta_{WN} = 1/3 \). Fründ (2021) measured \( \beta_{OS}=\beta_{ST}=1/6 \) and argued that it is appropriate insofar as it reflects that the number of unique links in the OS and ST components contributing to network dissimilarity (dashed lines) are actually equal. Conversely, the formula of Poisot et al. (2012) yields \( \beta_{OS}=1/5 \), hence \( \beta_{ST} = \frac{1}{3}-\frac{1}{5}=\frac{2}{15}<\beta_{OS} \). Fründ (2021) thus argued that the method of Poisot tends to underestimate the contribution of species turnover.
To clarify and avoid misinterpretation of the calculation of \( \beta_{OS} \) and \( \beta_{ST} \) in Poisot et al. (2012), Poisot (2022) provides a new, in-depth mathematical analysis of the decomposition of \( \beta_{WN} \). Poisot et al. (2012) quantify in \( \beta_{OS} \) the actual contribution of rewiring in network structure for the subweb of common species. Poisot (2022) thus argues that \( \beta_{OS} \) relates only to the probability of rewiring in the subweb, while the definition of \( \beta_{OS} \) by Fründ (2021) is relative to the count of interactions in the global network (considered in denominator), and is thereby dependent on both rewiring probability and species turnover. Poisot (2022) further clarifies the interpretation of \( \beta_{ST} \). \( \beta_{ST} \) is obtained by subtracting \( \beta_{OS} \) from \( \beta_{WN} \) and thus represents the influence of species turnover in terms of the relative architectures of the global networks and of the subwebs of shared species. Coming back to the example of Fig.1., the Poisot et al. (2012) formula posits that \( \frac{\beta_{ST}}{\beta_{WN}}=\frac{2/15}{1/3}=2/5 \), meaning that species turnover contributes two-fifths of change in network structure, while rewiring in the subweb of common species contributed three fifths. Conversely, the approach of Fründ (2021) does not compare the architectures of global networks and of the subwebs of shared species, but considers the relative contribution of unique links to network dissimilarity in terms of species turnover and rewiring.
Poisot (2022) concludes that the partition proposed in Fründ (2021) does not allow unambiguous ecological interpretation of rewiring. He provides guidelines for proper interpretation of the decomposition proposed in Poisot et al. (2012).
References
Fründ J (2021) Dissimilarity of species interaction networks: how to partition rewiring and species turnover components. Ecosphere, 12, e03653. https://doi.org/10.1002/ecs2.3653
Poisot T, Canard E, Mouillot D, Mouquet N, Gravel D (2012) The dissimilarity of species interaction networks. Ecology Letters, 15, 1353–1361. https://doi.org/10.1111/ele.12002
Poisot T (2022) Dissimilarity of species interaction networks: quantifying the effect of turnover and rewiring. EcoEvoRxiv Preprints, ver. 4 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.32942/osf.io/gxhu2
Beating your neighbor to the berry patch
When more competitors means less harvested resource
Recommended by François Munoz based on reviews by Francois Massol, Jeremy Van Cleve and 1 anonymous reviewerIn this paper, Alan R. Rogers (2021) examines the dynamics of foraging strategies for a resource that gains value over time (e.g., ripening fruits), while there is a fixed cost of attempting to forage the resource, and once the resource is harvested nothing is left for other harvesters. For this model, not any pure foraging strategy is evolutionary stable. A mixed equilibrium exists, i.e., with a mixture of foraging strategies within the population, which is still evolutionarily unstable. Nonetheless, Alan R. Rogers shows that for a large number of competitors and/or high harvesting cost, the mixture of strategies remains close to the mixed equilibrium when simulating the dynamics. Surprisingly, in a large population individuals will less often attempt to forage the resource and will instead “go fishing”. The paper also exposes an experiment of the game with students, which resulted in a strategy distribution somehow close to the theoretical mixture of strategies.
The economist John F. Nash Jr. (1950) gained the Nobel Prize of economy in 1994 for his game theoretical contributions. He gave his name to the “Nash equilibrium”, which represents a set of individual strategies that is reached whenever all the players have nothing to gain by changing their strategy while the strategies of others are unchanged. Alan R. Rogers shows that the mixed equilibrium in the foraging game is such a Nash equilibrium. Yet it is evolutionarily unstable insofar as a distribution close to the equilibrium can invade.
The insights of the study are twofold. First, it sheds light on the significance of Nash equilibrium in an ecological context of foraging strategies. Second, it shows that an evolutionarily unstable state can rule the composition of the ecological system. Therefore, the contribution made by the paper should be most significant to better understand the dynamics of competitive communities and their eco-evolutionary trajectories.
References
Nash JF (1950) Equilibrium points in n-person games. Proceedings of the National Academy of Sciences, 36, 48–49. https://doi.org/10.1073/pnas.36.1.48
Rogers AR (2021) Beating your Neighbor to the Berry Patch. bioRxiv, 2020.11.12.380311, ver. 8 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2020.11.12.380311

Soil variation response is mediated by growth trajectories rather than functional traits in a widespread pioneer Neotropical tree
Growth trajectories, better than organ-level functional traits, reveal intraspecific response to environmental variation
Recommended by François Munoz based on reviews by Georges Kunstler and François MunozFunctional traits are “morpho-physio-phenological traits which impact fitness indirectly via their effects on growth, reproduction and survival” [1]. Most functional traits are defined at organ level, e.g. for leaves, roots and stems, and reflect key aspects of resource acquisition and resource use by organisms for their development and reproduction [2]. More rarely, some functional traits can be related to spatial development, such as vegetative height and lateral spread in plants.
Organ-level traits are especially popular because they can be measured in a standard way and easily compared over many plants. But these traits can broadly vary during the life of an organism. For instance, Roggy et al. [3] found that Leaf Mass Area can vary from 30 to 140 g.m^(-2) between seedling and adult stages for the canopy tree Dicorynia guianensis in French Guiana. Fortunel et al. [4] have also showed that developmental stages much contribute to functional trait variation within several Micropholis tree species in lowland Amazonia.
The way plants grow and invest resources into organs is variable during life and allows defining specific developmental sequences and architectural models [5,6]. There is clear ontogenic variation in leaf number, leaf properties and ramification patterns. Ontogenic variations reflect changing adaptation of an individual over its life, depending on the changing environmental conditions.
In this regard, measuring a single functional trait at organ level in adult trees should miss the variation of resource acquisition and use strategies over time. Thus we should built a more integrative approach of ecological development, also called “eco-devo” approach [7].
Although the ecological significance of ontogeny and developmental strategies is now well known, the extent to which it contributes to explain species survival and coexistence in communities is still broadly ignored in functional ecology. Levionnois et al. [8] investigated intraspecific variation of functional traits and growth trajectories in a typical, early-successional tree species in French Guiana, Amazonia. This species, Cecropia obtusa, is generalist regarding soil type and can be found on both white sand and ferralitic soil. The study examines whether there in intraspecific variation in functional traits and growth trajectories of C. obtusa in response to the contrasted soil types.
The tree communities observed on the two types of soils include species with distinctive functional trait values, that is, there are changes in species composition related to different species strategies along the classical wood and leaf economic spectra. The populations of C. obtusa found on the two soils showed some difference in functional traits, but it did not concern traits related to the main economic spectra. Conversely, the populations showed different growth strategies, in terms of spatial and temporal development.
The major lessons we can learn from the study are:
(i) Functional traits measured at organ level cannot reflect well how long-lived plants collect and invest resources during their life. The results show the potential of considering architectural and developmental traits together with organ-level functional traits, to better acknowledge the variation in ecological strategies over plant life, and thus to better understand community assembly processes.
(ii) What makes functional changes between communities differs when considering interspecific and intraspecific variation. Species turnover should encompass different corteges of soil specialists. These specialists are sorted along economic spectra, as shown in tropical rainforests and globally [2]. Conversely, a generalist species such as C. obtusa does occur on contrasted soil, which entails that it can accommodate the contrasted ecological conditions. However, the phenotypic adjustment is not related to how leaves and wood ensure photosynthesis, water and nutrient acquisition, but regards the way the resources are allocated to growth and reproduction over time.
The results of the study stress the need to better integrate growth strategies and ontogeny in the research agenda of functional ecology. We can anticipate that organ-level functional traits and growth trajectories will be more often considered together in ecological studies. The integration should help better understand the temporal niche of organisms, and how organisms can coexist in space and time with other organisms during their life. Recently, Klimešová et al. [9] have proposed standardized protocols for collecting plant modularity traits. Such effort to propose easy-to-measure traits representing plant development and ontogeny, with clear functional roles, should foster the awaited development of an “eco-devo” approach.
References
[1] Violle, C., Navas, M. L., Vile, D., Kazakou, E., Fortunel, C., Hummel, I., & Garnier, E. (2007). Let the concept of trait be functional!. Oikos, 116(5), 882-892. doi: 10.1111/j.0030-1299.2007.15559.x
[2] Díaz, S. et al. (2016). The global spectrum of plant form and function. Nature, 529(7585), 167-171. doi: 10.1038/nature16489
[3] Roggy, J. C., Nicolini, E., Imbert, P., Caraglio, Y., Bosc, A., & Heuret, P. (2005). Links between tree structure and functional leaf traits in the tropical forest tree Dicorynia guianensis Amshoff (Caesalpiniaceae). Annals of forest science, 62(6), 553-564. doi: 10.1051/forest:2005048
[4] Fortunel, C., Stahl, C., Heuret, P., Nicolini, E. & Baraloto, C. (2020). Disentangling the effects of environment and ontogeny on tree functional dimensions for congeneric species in tropical forests. New Phytologist. doi: 10.1111/nph.16393
[5] Barthélémy, D., & Caraglio, Y. (2007). Plant architecture: a dynamic, multilevel and comprehensive approach to plant form, structure and ontogeny. Annals of botany, 99(3), 375-407. doi: 10.1093/aob/mcl260
[6] Hallé, F., & Oldeman, R. A. (1975). An essay on the architecture and dynamics of growth of tropical trees. Kuala Lumpur: Penerbit Universiti Malaya.
[7] Sultan, S. E. (2007). Development in context: the timely emergence of eco-devo. Trends in Ecology & Evolution, 22(11), 575-582. doi: 10.1016/j.tree.2007.06.014
[8] Levionnois, S., Tysklind, N., Nicolini, E., Ferry, B., Troispoux, V., Le Moguedec, G., Morel, H., Stahl, C., Coste, S., Caron, H. & Heuret, P. (2020). Soil variation response is mediated by growth trajectories rather than functional traits in a widespread pioneer Neotropical tree. bioRxiv, 351197, ver. 4 peer-reviewed and recommended by PCI Ecology. doi: 10.1101/351197
[9] Klimešová, J. et al. (2019). Handbook of standardized protocols for collecting plant modularity traits. Perspectives in Plant Ecology, Evolution and Systematics, 40, 125485. doi: 10.1016/j.ppees.2019.125485