
How to evaluate and interpret the contribution of species turnover and interaction rewiring when comparing ecological networks?
 based on reviews by Ignasi Bartomeus and 1 anonymous reviewer
based on reviews by Ignasi Bartomeus and 1 anonymous reviewer

Dissimilarity of species interaction networks: quantifying the effect of turnover and rewiring
Abstract
Recommendation: posted 28 February 2022, validated 01 March 2022
Munoz, F. (2022) How to evaluate and interpret the contribution of species turnover and interaction rewiring when comparing ecological networks?. Peer Community in Ecology, 100092. https://doi.org/10.24072/pci.ecology.100092
Recommendation
A network includes a set of vertices or nodes (e.g., species in an interaction network), and a set of edges or links (e.g., interactions between species). Whether and how networks vary in space and/or time are questions often addressed in ecological research.
Two ecological networks can differ in several extents: in that species are different in the two networks and establish new interactions (species turnover), or in that species that are present in both networks establish different interactions in the two networks (rewiring). The ecological meaning of changes in network structure is quite different according to whether species turnover or interaction rewiring plays a greater role. Therefore, much attention has been devoted in recent years on quantifying and interpreting the relative changes in network structure due to species turnover and/or rewiring.
Poisot et al. (2012) proposed to partition the global variation in structure between networks, \( \beta_{WN} \) (WN = Whole Network) into two terms: \( \beta_{OS} \) (OS = Only Shared species) and \( \beta_{ST} \) (ST = Species Turnover), such as \( \beta_{WN} = \beta_{OS} + \beta_{ST} \).
The calculation lays on enumerating the interactions between species that are common or not to two networks, as illustrated on Figure 1 for a simple case. Specifically, Poisot et al. (2012) proposed to use a Sorensen type measure of network dissimilarity, i.e., \( \beta_{WN} = \frac{a+b+c}{(2a+b+c)/2} -1=\frac{b+c}{2a+b+c} \) , where \( a \) is the number of interactions shared between the networks, while \( b \) and \( c \) are interaction numbers unique to one and the other network, respectively. \( \beta_{OS} \) is calculated based on the same formula, but only for the subnetworks including the species common to the two networks, in the form \( \beta_{OS} = \frac{b_{OS}+c_{OS}}{2a_{OS}+b_{OS}+c_{OS}} \) (e.g., Fig. 1). \( \beta_{ST} \) is deduced by subtracting \( \beta_{OS} \) from \( \beta_{WN} \) and represents in essence a "dissimilarity in interaction structure introduced by dissimilarity in species composition" (Poisot et al. 2012).
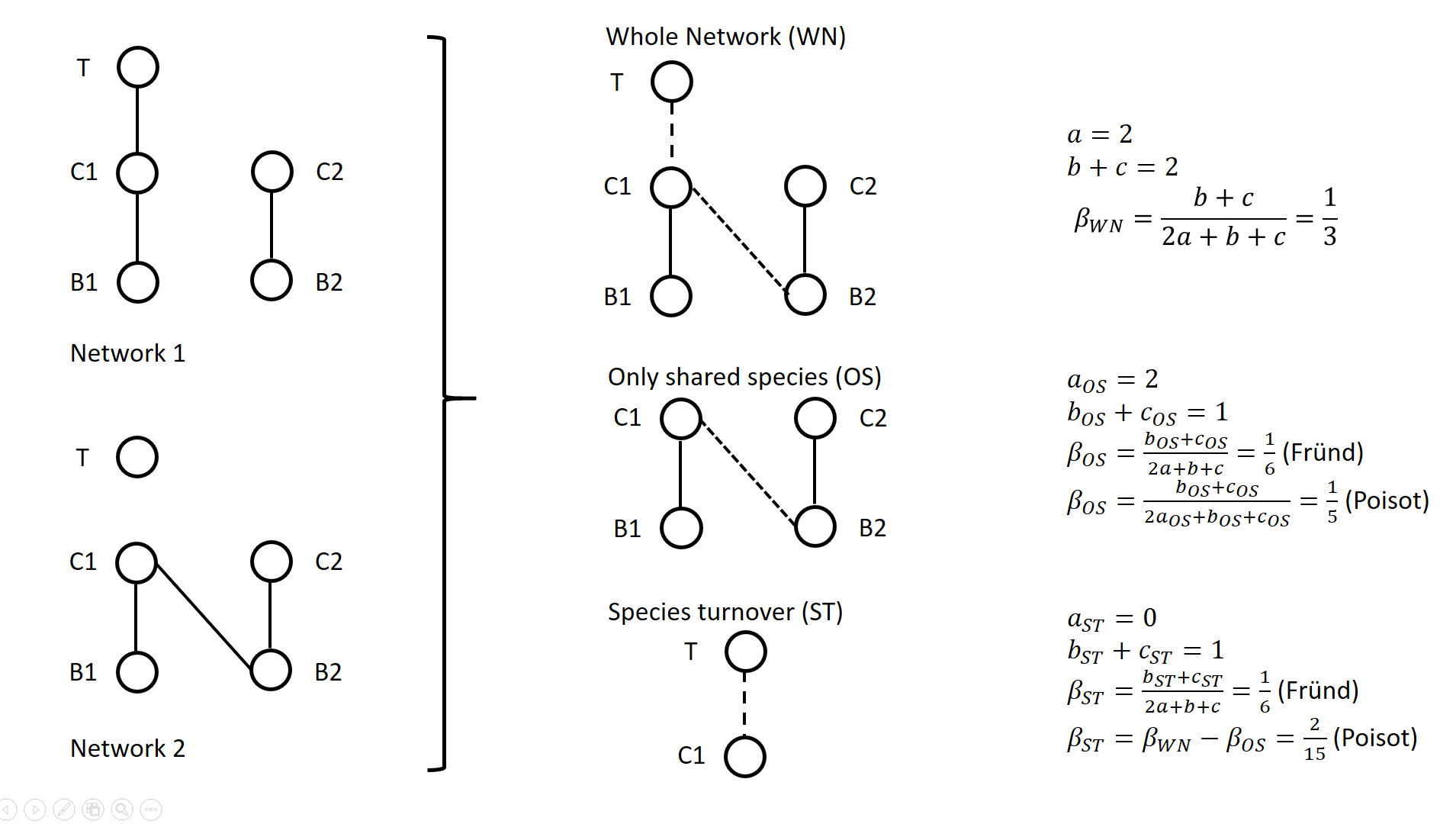
Figure 1. Ecological networks exemplified in Fründ (2021) and discussed in Poisot (2022). a is the number of shared links (continuous lines in right figures), while b+c is the number of edges unique to one or the other network (dashed lines in right figures).
Alternatively, Fründ (2021) proposed to define \( \beta_{OS} = \frac{b_{OS}+c_{OS}}{2a+b+c} \) and \( \beta_{ST} = \frac{b_{ST}+c_{ST}}{2a+b+c} \), where \( b_{ST}=b-b_{OS} \) and \( c_{ST}=c-c_{OS} \) , so that the components \( \beta_{OS} \) and \( \beta_{ST} \) have the same denominator. In this way, Fründ (2021) partitioned the count of unique \( b+c=b_{OS}+b_{ST}+c_{ST} \) interactions, so that \( \beta_{OS} \) and \( \beta_{ST} \) sums to \( \frac{b_{OS}+c_{OS}+b_{ST}+c_{ST}}{2a+b+c} = \frac{b+c}{2a+b+c} = \beta_{WN} \). Fründ (2021) advocated that this partition allows a more sensible comparison of \( \beta_{OS} \) and \( \beta_{ST} \), in terms of the number of links that contribute to each component.
For instance, let us consider the networks 1 and 2 in Figure 1 (left panel) such as \( a_{OS}=2 \) (continuous lines in right panel), \( b_{ST} + c_{ST} = 1 \) and \( b_{OS} + c_{OS} = 1 \) (dashed lines in right panel), and thereby \( a = 2 \), \( b+c=2 \), \( \beta_{WN} = 1/3 \). Fründ (2021) measured \( \beta_{OS}=\beta_{ST}=1/6 \) and argued that it is appropriate insofar as it reflects that the number of unique links in the OS and ST components contributing to network dissimilarity (dashed lines) are actually equal. Conversely, the formula of Poisot et al. (2012) yields \( \beta_{OS}=1/5 \), hence \( \beta_{ST} = \frac{1}{3}-\frac{1}{5}=\frac{2}{15}<\beta_{OS} \). Fründ (2021) thus argued that the method of Poisot tends to underestimate the contribution of species turnover.
To clarify and avoid misinterpretation of the calculation of \( \beta_{OS} \) and \( \beta_{ST} \) in Poisot et al. (2012), Poisot (2022) provides a new, in-depth mathematical analysis of the decomposition of \( \beta_{WN} \). Poisot et al. (2012) quantify in \( \beta_{OS} \) the actual contribution of rewiring in network structure for the subweb of common species. Poisot (2022) thus argues that \( \beta_{OS} \) relates only to the probability of rewiring in the subweb, while the definition of \( \beta_{OS} \) by Fründ (2021) is relative to the count of interactions in the global network (considered in denominator), and is thereby dependent on both rewiring probability and species turnover. Poisot (2022) further clarifies the interpretation of \( \beta_{ST} \). \( \beta_{ST} \) is obtained by subtracting \( \beta_{OS} \) from \( \beta_{WN} \) and thus represents the influence of species turnover in terms of the relative architectures of the global networks and of the subwebs of shared species. Coming back to the example of Fig.1., the Poisot et al. (2012) formula posits that \( \frac{\beta_{ST}}{\beta_{WN}}=\frac{2/15}{1/3}=2/5 \), meaning that species turnover contributes two-fifths of change in network structure, while rewiring in the subweb of common species contributed three fifths. Conversely, the approach of Fründ (2021) does not compare the architectures of global networks and of the subwebs of shared species, but considers the relative contribution of unique links to network dissimilarity in terms of species turnover and rewiring.
Poisot (2022) concludes that the partition proposed in Fründ (2021) does not allow unambiguous ecological interpretation of rewiring. He provides guidelines for proper interpretation of the decomposition proposed in Poisot et al. (2012).
References
Fründ J (2021) Dissimilarity of species interaction networks: how to partition rewiring and species turnover components. Ecosphere, 12, e03653. https://doi.org/10.1002/ecs2.3653
Poisot T, Canard E, Mouillot D, Mouquet N, Gravel D (2012) The dissimilarity of species interaction networks. Ecology Letters, 15, 1353–1361. https://doi.org/10.1111/ele.12002
Poisot T (2022) Dissimilarity of species interaction networks: quantifying the effect of turnover and rewiring. EcoEvoRxiv Preprints, ver. 4 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.32942/osf.io/gxhu2
The recommender in charge of the evaluation of the article and the reviewers declared that they have no conflict of interest (as defined in the code of conduct of PCI) with the authors or with the content of the article. The authors declared that they comply with the PCI rule of having no financial conflicts of interest in relation to the content of the article.
Evaluation round #2
DOI or URL of the preprint: https://doi.org/10.32942/osf.io/gxhu2
Version of the preprint: 2
Author's Reply, 13 Dec 2021
I have addressed all comments by reviewer 1; the points that they thought were more important have been brought up immediately upon introducing the components of the beta diversity decomposition. All other minor comments have been fixed.
Decision by François Munoz , posted 02 Dec 2021
, posted 02 Dec 2021
Dear Timothée,
The reviewers and me are happy with the new version of the manuscript, which acknowledges well the previous comments and suggestions.
I would invite you to perform minor revision of the manuscript, by taking into account the points made by reviewer 1.
Best wishes,
François
Reviewed by anonymous reviewer 1, 10 Nov 2021
The revised version of this manuscript addresses all points I made on the previous draft.
https://doi.org/10.24072/pci.ecology.100331.rev21Reviewed by Ignasi Bartomeus , 22 Nov 2021
, 22 Nov 2021
I thank the author for extensive re-writing of the text, including the new section with guidelines on how to use beta-diversity metrics. This new version is very illustrative and easy to follow. I don't have any further important comments on the manuscript, but given that people tend to read papers rapidly, I would suggest highlighting two key lines that are now a bit buried in the middle of paragraphs. Those are line 230: "It is paramount to clarify that 𝛽𝑠𝑡 is not a direct measure of the importance of turnover: it is a quantification of the relative impact of rewiring to overall dissimilarity" and line 261: "the very point of the approach is to provide measures that can be interpreted in the light of connectance and species turnover." To me, those are the two most common misunderstandings in the literature, and it would be great to make them cristal clear in abstract and/or final guidelines. If people correctly understand BestaST and interpret the beta-diversity metrics along with other network properties, and not as stand-alone products, this paper will make a great contribution.
In addition, there are a few comments regarding formating:
Line 34: maybe "fig 1" should go between brackets?
Line 104: Is this reference correct? (Bezanson2017JulFre?)
Eq line 111: why the subindex t?
Line 120: U is a given subset of links? Or I am missing something.
Line 134: The equations and rationale are clear here, but why do you mention A, S and U? Where do those come from? They appear again in line 138, but I miss where they are introduced initially.
Best,
Ignasi Bartomeus
https://doi.org/10.24072/pci.ecology.100331.rev22Evaluation round #1
DOI or URL of the preprint: 10.32942/osf.io/gxhu2
Version of the preprint: 1
Author's Reply, 26 Oct 2021
Decision by François Munoz , posted 20 Sep 2021
, posted 20 Sep 2021
Dear Timothée,
We have received two detailed and insightful reviews of the preprint you have submitted to PCI Ecology.
I would like that you carefully revise the manuscript according to the comments and suggestions.
The most salient point is that the preprint is a kind of response/comment to a recent paper of Fründ in Ecosphere.
In addition, the ms does not follow a classical Introduction/M&M/Results/Discussion section, arguably because of the response/comment nature of this contribution.
As suggested by reviewer 2, the ms would gain clarity if,
-an Introduction section more explicitly states the nature of the diverging views between Fründ and you, and thus more clearly exposing the motivation of challenging the recent paper of Fründ,
-a Discussion section synthesizes the pros and cons of both approaches, as it seems that each method can be justified and used in an appropriate context.
Thank you for considering PCI Ecology as a venue for your work, and we look forward to receiving your revised manuscript.
Sincerely,
François
Download recommender's annotationsReviewed by Ignasi Bartomeus , 19 Aug 2021
, 19 Aug 2021
While there is no doubt that partitioning interaction turnover is a needed tool for ecologists, there has been recent debate on how to best perform this partitioning. I assess this manuscript from the perspective of the interested user in applying such indexes and doing it correctly. This means that while I mostly follow the maths decomposing the different indexes, I focus my review on their interpretation, and I can't fully assess the more complex mathematical derivations.
I appreciate the detailed explanation provided and the rationale behind each index. I think the calculation and interpretation of BetaOS are clear. This one can be interpreted unambiguously as interaction rewiring among shared species. To me, this is the key index to interpret for most ecological questions and can be interpreted as a single index (probably along with the proportion of shared species for context).
Next, Beta WN is also intuitive, but as depicted in Fig 2 it needs to be clearly stated that it depends on both interaction rewiring and the proportion of shared species. For most ecological questions it may be of secondary importance.
The most problematic term for me is BetaST. This is also stated in the manuscript, and I agree that it has caused a larger degree of confusion. Interpreting this term (beyond an error term, which is the simplest interpretation) is complex. In fact, the manuscript often describes their behaviour as "as expected" given its mathematical formulation, but looking at the literature it is clear that most researchers (including myself) were not expecting some of those behaviours. However, even when completely understanding how it behaves, the interpretation is still too complex for me in order to be useful. Fig 2 B is ilustrative to me. Note that at q = 1; BetaST = 0 regardless of the proportion of species sharing! Hence, BetaST tells you nothing about the contribution of species turnover when rewiring is high (ST stands for species turnover, so it's normal people get confused). I had this discussion with several researchers, and I can tell this is hard to grasp at first. Following with figure 2B, you can see that the same value can mean two very different things. BetaST can be low if there is high rewiring, or if rewiring is very low, but they share most species. This is less accentuated in the relative importance but is still the case. Hence, I would suggest giving clear recommendations on not interpreting BetaST as a primary index, but only in cases when is pertinent, and giving a clear context (i.e. the proportion of shared species, which I think is much more useful for ecological questions). I know this is suggested in some places of the manuscript, but in my opinion, it can be said stronger. In fact, I would love to see a section on how to interpret each component, recommending the interpretation of BetaOS as the most straightforward, and cautioning that interpretation of beta WN, and especially ST need to be done in context and can't be interpreted alone.
Other than this, I have some minor comments:
line 13: Currently it is done in several ways, so maybe better cite here Poisot et al 2012.
line 15-21: This is a very long sentence with "i.e", ";", "-", which I had to read twice. Consider splitting it up. At least a point after "Tuomisto 2010)" I think is needed.
lines 72-74: letters used in the text do not match those in the equation. (m = k, I think)
line 85: The second "similarly" can be replaced by "also".
line 98: I would name between brackets the abbreviations of Sorensen and Wittaker indexes when first mentioned a couple of lines above.
line 111-112: I think the reader needs first to be introduced briefly to what Frund did differently to understand this sentence. This is not done until line 160.
line 150: I understand we do not need species yet, but this first numerical exercise is quite abstract. Maybe guide the reader on the purpose of the experiment. Which I believe is to describe the behaviour of the components.
line 165: I agree with this interpretation "it is a quantification of the relative impact of rewiring to overall dissimilarity". My critique is that this measure, as defined here, is hard to interpret ecologically and I may dare to say that irrelevant for most ecological questions.
Line 165: But I do not follow the next sentence. What do you mean by "all non-turnover mechanisms being accounted for in the decomposition, can be explained by turnover mechanisms". See my point above on the ambiguity of interpreting its values, which can emerge from very different ecological situations.
line 171: Adding the illustration may help a lot. I had to write it myself (and it was not easy for me).
line 228: formatting error when designing the title.
Fig 3: Maybe expressing the x-axes as connectance dissimilarity would help the reader? I would also appreciate a comment in the text on further partitioning of the components on changes due to differences in link number (related to connectance) and true link turnover. Those are discussed by Frund, and I think it can help interpret those values depending on your ecological question.
line 260: Here a caution on interpreting BetaST may be good as stated above.
Best,
Ignasi Bartomeus
Reviewed by anonymous reviewer 1, 14 Sep 2021
General comments
The paper is dedicated to an outstanding question, how to compare interaction networks teasing apart the effect of species turnover and interaction rewiring. This question is central in many studies, due to the recent development of efficient data acquisition techniques in the "multiple networks era".
The author did not write a cover letter. It would have been important in particular regarding the following observations. From the last paragraph of the first section, we early understand that this manuscript is actually responding another, Fründ 2021, that gave some objective criticisms about the renowed method developed by the author of the present manuscript in Poisot et al 2011. In my opinion, the abstract is not clear about this fact because it does not clearly state the debate which is central in the paper, i.e. the different views proposed by Fründ and Poisot respectively. Indeed, having read the paper by Fründ seems to be a prerequisite to read this manuscript. The paper does not have a classical structure with the usual sections (e.g. no "Introduction/Discussion" keywords) but is linear in the sense that the arguments are displayed one after the other. Again, this is not clear enough to easily see 1/ what is exactly the debate 2/ what is the author's strategy to convince the reader in this debate. Finally, the notations adopted in this manuscript are completely different from those of Fründ, which does not help the reader in evaluating the different conclusions raised by both authors.
About the numerical experiments, they are well conducted and clear but could be better motivated. The first one consists in redoing the small example proposed in Fründ (here, this is clear). The conclusion is that actually both authors have two different understanding of the betast but in fact the actual incoherence between the two authors comes from the fact that Poisot counts the shared interactions twice, which is actually not an issue as long as the network is large enough. The next two experiments are dedicated to bipartite networks : what is the reason for this choice? In fact, one can question the generalisability of the conclusions to unipartite networks. The first one explores the variation of the different beta measures with rewiring and turnover, and actually shows these measures are responding as expected. The second one is investigating the possible link between the beta measures and connectance. In fact, it is clear that connectance difference can induce a large dissimilarity between two networks (again, not only bipartite networks). The author shows his results for two connectance values in the bipartite case, but one can expect a broader exploration of the link between intrinsic networks properties (for a range of variation, not two values) and the beta measures. Connectance is indeed important, but degree distribution is paramount as well (at a fixed connectance, for instance). Finally the author gives his opinion about the need for a new denominator as suggested by Fründ. However, the previous experiments were not performed with an alternative denominator, and then the reader can not compare different proposals.
The paper is, again, dealing with an outstanding question using very important methodology. But the reader could expect more systematic experiments (unipartite case?) and a better organized manuscript.
As a minor point, I would like to mention that the paper include as series of typo errors.
Line by line comments
In the following, I give a list of comments. I hope they can help improving the manuscript.
L.32 Maybe citing Ohlman et al, Eco. Lett. as another extension.
L.53 Typo "baed"
L.54 Using "x" here and then using "x" L.56-57 could be misleading. Maybe just say "|.|" is the cardinality operator ?
L.66-68 This assumes that edges are directed. This can not be the case, for mutualistic interaction (btw, replacing an undirected edge by two directed edges is still possible)
L.70 Well, classically, Vm are the vertices of m (all of them)...
L.70 Is Ec with "c" for "in common"? If yes, tell it because it can help memorizing.
L.71 Typo: capital N instead of capital M.
L.87 In my opinion, that's a good point to call it "rewiring".
L.89 a is supposed to be the union, and Ec is the intersection. Is there a problem here in the analogy? Maybe I missed something, my apologies in advance.
Also, a/b/c are supposed to be cardinality, and this is not the case in the table. Am I right?
L.98 betaSor and betaw, betat not defined before.
L.98 Typo : where is (i) ?
L.93-102 This paragraph is difficult to understand without being an expert of the mentioned papers. What is the message here?
L.104 OK, here betat is defined. This is related to Dice (1945) or Sorensen (1948)?
L.111-112 "they are using components of the networks that are not part of the networks being compared" is not clear.
L.114 Which calculation?
L.113-121 This part of the paper looks like an answer to Fründ. Is this an "answer" paper ?
L.120 Typo : "very point"
L.130-143 Straightforward mathematics, details could go in appendix.
L.151 Once again, the choice of these capital letters for shared (A), rewired (S), and unique (U) does not help.
L.151 In fact, ps is a proportion but pr is not, whereas pr X (1-ps) is a proportion... (pr is a proportion of the proportion of non-shared links).
L.153 How can "shared links [be] rewired" if they are shared?
L.164-166 Maybe split this 3 lines sentence, to facilitate understanding ?
L.176 Precise what are these three-fifth (this is because betast/betawn=2/5)
L.178 This "2A" is the key point. This is enough to understand the full paragraph.
L.182 Then, should we move to such a measure that do not amplify the effect of rewiring?
L.184 Why do we switch to bipartite networks here ?
L.184 Again, the choice of capital R for a number of species could be discussed.
L.196-199 Are these conclusions not obvious ? From the definitions of the beta indices.
L.197 Previously, we have "proportions" and now we have "probabilities". It would be better to harmonize.
Figure2 Please harmonize the axis labels with Figure 1.
L.208-209 Typo: bad copy/paste here.
L.210 Again, why bipartite networks? Also, why varying connectance? It is a relevant idea but one can make the degree distribution vary as well. This distribution can have huge impacts on beta indices.
Also, it is normal to expect huge dissimilarity between network of different connectance because the number of un-shared links is expected to be high. This seems straighforward.
Here, the reader can expect a formulation of the hypothesis that will be tested : what is this numerical experiment for?
L.243 The formulation "I do not think" is not appropriate because the reader will not expect an opinion but conclusions drawn for the previous experiments.
L.244 It would be necessary to recall the proposal of Fründ somewhere in the paper. Did the author perform the same numerical experiments with the other numerator?
L.246 "rigorous definition of networks as graphs (as opposed to networks as matrices)". It is unclear why we have to oppose the matrix and the graph view, since graphs and adjacency matrices belong to the same conceptual context.
L.252-254 In fact, one can think that the debate is solved by choising a definition. A matter of perspective, at some point.
https://doi.org/10.24072/pci.ecology.100331.rev12









