Understanding the effects of environmental perturbations on coexistence is a key challenge in ecology, and models have played an important role in structuring our ideas and generating predictions, leading to quantitative hypotheses. In such models, environmental perturbations are often captured by changes in parameter values, such as the intrinsic growth rates of species (1–3). The question then becomes how much one can change these parameters without breaking coexistence and thus losing species (4). 
 
An intuitively appealing approach to address this question is to calculate a model’s feasibility domain (5–7). Loosely defined, it is the fraction of parameter settings leading to the coexistence of all species. Mathematically speaking, it is a high-dimensional triangle, of which one can calculate the size, just as for plain two-dimensional triangles. Parameter settings outside of this triangle break coexistence. Thus, it seems logical that greater feasibility domains would make for more robust ecosystems. However, careful interpretation is key: a greater feasibility domain merely implies that across many attempts at running a model with different random parameter settings, coexistence will be more frequent. It does not necessarily inform us how much one can perturb the parameters of a community with a predefined parameter setting. To get this information, we also need to know the shape of the triangle (7): perturbations more easily knock the parameter setting out of a flat triangle than out of an equilateral triangle. 
 
Desaillais et al. (8) develop a new theory that sheds light on what drives the shape of the feasibility domain. Specifically, they present the probability distribution that tells how close to the edge of the feasibility domain the parameter settings in that domain tend to be. For example, all points in a very flat triangle are close to its edge, while in an equilateral triangle, most points are safely stowed inside. The results show how, in a Lotka-Volterra model, the matrix of species interactions fully defines this distribution, which makes the technique empirically applicable in so far as one can estimate these interactions. The analysis then continues to explore the role of specific species in putative loss of coexistence. Desaillais et al. identify two species-level quantities: the first measures the total influence of the surrounding community on a focal species, while the second is a proxy for how close that focal species is to being lost, should a perturbation occur. While these two quantities are not mathematically independent, their correlation is not perfect, allowing one to categorize species into distinct ecological roles. A dataset of plant communities with different compositions illustrates how to apply this idea and gain some additional insight into the robustness of coexistence. These results pave the way for a number of potentially rewarding applications. How does the robustness of coexistence differ across network types? For which network types do we find back a more diverse set of ecological roles for species, i.e. for which networks are the two quantities least correlated? 

References

1. Baert, J.M., Janssen, C.R., Sabbe, K., and De Laender, F. (2016). Per capita interactions and stress tolerance drive stress-induced changes in biodiversity effects on ecosystem functions. Nat. Commun. 7, 12486. https://doi.org/10.1038/ncomms12486

2. Pásztor, L., Botta-Dukat, Z., Magyar, G., Czaran, T., and Meszéna, G. (2016). Theory-based ecology: A Darwinian approach 1st ed. (Oxford University Press).

3. Cenci, S., Montero-Castaño, A., and Saavedra, S. (2018). Estimating the effect of the reorganization of interactions on the adaptability of species to changing environments. J. Theor. Biol. 437, 115–125. https://doi.org/10.1016/j.jtbi.2017.10.016

4. Spaak, J.W., Baert, J.M., Baird, D.J., Eisenhauer, N., Maltby, L., Pomati, F., Radchuk, V., Rohr, J.R., Van den Brink, P.J., and De Laender, F. (2017). Shifts of community composition and population density substantially affect ecosystem function despite invariant richness. Ecol. Lett. 20, 1315–1324. https://doi.org/10.1111/ele.12828

5. Meszéna, G., Gyllenberg, M., Pásztor, L., and Metz, J.A.J. (2006). Competitive exclusion and limiting similarity: A unified theory. Theor. Popul. Biol. 69, 68–87. https://doi.org/10.1016/j.tpb.2005.07.001

6. Saavedra, S., Rohr, R.P., Bascompte, J., Godoy, O., Kraft, N.J.B., and Levine, J.M. (2017). A structural approach for understanding multispecies coexistence. Ecol. Monogr. 87, 470–486. https://doi.org/10.1002/ecm.1263

7. Grilli, J., Adorisio, M., Suweis, S., Barabás, G., Banavar, J.R., Allesina, S., and Maritan, A. (2017). Feasibility and coexistence of large ecological communities. Nat. Commun. 8. https://doi.org/10.1038/ncomms14389

8. Desallais M, Loreau M, Arnoldi J.F. (2024) The distribution of distances to the edge of species coexistence. bioRxiv, ver.4 peer-reviewed and recommended by PCI Ecology https://doi.org/10.1101/2024.01.21.575550

The output of a community model depends on how you set its parameters. Thus, analyses of specific parameter settings hardwire the results to specific ecological scenarios. Because more general answers are often of interest, one tradition is to give models a statistical treatment: one summarizes how model parameters vary across species, and then predicts how changing the summary, instead of the individual parameters themselves, would change model output. Arguably the best-known example is the work initiated by May, showing that the properties of a community matrix, encoding effects species have on each other near their equilibrium, determine stability (1,2). More recently, this statistical treatment has also been applied to one of community ecology’s more prickly and slippery subjects: community assembly, which deals with the question “Given some regional species pool, which species will be able to persist together at some local ecosystem?”. Summaries of how species grow and interact in this regional pool predict the fraction of survivors and their relative abundances, the kind of dynamics, and various kinds of stability (3,4). One common characteristic of such statistical treatments is the assumption of disorder: if species do not interact in too structured ways, simple and therefore powerful predictions ensue that often stand up to scrutiny in relatively ordered systems. 
 
In their recent preprint, Miller, Clenet, et al. (5) subscribe to this tradition and consider tractable assembly scenarios (6) to study the outcome of assembly in a metacommunity. They recover a result of remarkable simplicity: roughly half of the species pool makes it into the final assemblage. Their vehicle is Tilman’s classic metacommunity model (7), where colonization rates are traded off with competitive ability. More precisely, in this model, one ranks species according to their colonization rate and attributes a greater competitive strength to lower-ranked species, which makes competition strictly hierarchical and thus departs from the disorder usually imposed by statistical approaches. The authors then leverage the simplicity of the species interaction network implied by this recursive setting to analytically probe how many species survive assembly. This turns out to be a fixed fraction that is distributed according to a Binomial with a mean of 0.5. While these results should not be extrapolated beyond the system at hand (4), they are important for two reasons. First, they imply that, within the framework of metacommunities driven by competition-colonization tradeoffs, richer species pools will produce richer communities: there is no upper bound on species richness, other than the one set by the raw material available for assembly. Second, this conclusion does not rely on simulation or equation solving and is, therefore, a hopeful sign of the palatability of the problem, if formalized in the right way. Their paper then shows that varying some of the settings does not change the main conclusion: changing how colonization rates distribute across species, and therefore the nature of the tradeoff, or the order with which species invade seems not to disrupt the big picture. Only when invaders are created “de novo” during assembly, a scenario akin to “de novo” mutation, a smaller fraction of species will survive assembly. 
 
As always, logical extensions of this study involve complicating the model and then looking if the results stay on par. The manuscript cites switching to other kinds of competition-colonization tradeoffs, and the addition of spatial heterogeneity as two potential avenues for further research. While certainly of merit, alternative albeit more bumpy roads would encompass models with radically different behavior. Most notably, one wonders how priority effects would play out. The current analysis shows that different invasion orders always lead to the same final composition, and therefore the same final species richness, confirming earlier results from models with similar structures (6). In models with priority effects, different invasion orders will surely lead to different compositions at the end. However, if one only cares about how many (and not which) species survive, it is unsure how much priority effects will qualitatively affect assembly. Because priority effects are varied in their topological manifestation (8), an important first step will be to evaluate which kinds of priority effects are compliant with formal analysis. 
 
References
 
1. May, R. M. (1972). Will a Large Complex System be Stable? Nature 238, 413–414. https://doi.org/10.1038/238413a0

2. Allesina, S. & Tang, S. (2015). The stability–complexity relationship at age 40: a random matrix perspective. Population Ecology, 57, 63–75. https://doi.org/10.1007/s10144-014-0471-0

3. Bunin, G. (2016). Interaction patterns and diversity in assembled ecological communities. Preprint at http://arxiv.org/abs/1607.04734.

4. Barbier, M., Arnoldi, J.-F., Bunin, G. & Loreau, M. (2018). Generic assembly patterns in complex ecological communities. Proceeding of the National Academy of Sciences, 115, 2156–2161. https://doi.org/10.1073/pnas.1710352115

5. Miller, Z. R., Clenet, M., Libera, K. D., Massol, F. & Allesina, S. (2023). Coexistence of many species under a random competition-colonization trade-off. bioRxiv 2023.03.23.533867, ver 3 peer-reviewed and recommended by PCI Ecology. https://doi.org/10.1101/2023.03.23.533867

6. Serván, C. A. & Allesina, S. (2021). Tractable models of ecological assembly. Ecology Letters, 24, 1029–1037. https://doi.org/10.1111/ele.13702

7. Tilman, D. (1994). Competition and Biodiversity in Spatially Structured Habitats. Ecology, 75, 2–16. https://doi.org/10.2307/1939377

8. Song, C., Fukami, T. & Saavedra, S. (2021). Untangling the complexity of priority effects in multispecies communities. Ecolygy Letters, 24, 2301–2313. https://doi.org/10.1111/ele.13870

Biodiversity loss can have important consequences for ecosystem functions, as exemplified by a large body of literature spanning at least three decades [1–3]. While connections between species diversity and ecosystem functions are now well-defined and understood, the importance of diversity within species is more elusive. Despite a surge in theoretical work on how intraspecific diversity can affect coexistence in simple community types [4,5], not much is known about how intraspecific diversity drives ecosystem processes in more complex community types. One particular challenge is that intraspecific diversity can be expressed as observable variation of functional traits, or instead subsist as genetic variation of which the consequences for ecosystem processes are harder to grasp.
Raffard et al. [6] examined how intraspecific biodiversity loss in a consumer fish changes species diversity at lower trophic levels and ecosystem processes in pond mesocosms. An interesting feature of this experiment is that it crosses functional and genetic intraspecific diversity. To do so, Raffard and colleagues measured and genotyped European minnow (P. phoxinus) individuals sampled from streams across southern France. Combining these collected specimens into experimental ponds allowed them to control functional (population variance of body size) and genetic intraspecific richness (number of genotypes).
Effects on minnow biomass production were mostly small; biomass was significantly reduced only when lowering both functional and genetic richness. However, the consequences for lower trophic levels (zooplankton and macroinvertebrates) were more pronounced and – importantly – not intuitive. For instance, the macroinvertebrate community was less species-diverse at higher minnow functional richness. If minnows with different body sizes would be the main regulator factors [7] explaining macroinvertebrate interactions, one would expect a more diverse set of minnow body sizes (i.e. higher functional minnow richness) to permit higher instead of lower macroinvertebrate richness. At the same time, the macroinvertebrate community was more species-diverse at higher minnow genotype richness, which could indicate unobserved minnow traits determining macroinvertebrate diversity more than the usual suspects (functional consumer richness). Such unobserved traits could be behavioral traits, allowing for resource partitioning among fish.
The consequences of functional minnow diversity loss on zooplankton diversity were negative, as expected in case body size differences among fish would facilitate coexistence of their zooplankton prey, as explained above. However, this was only the case when genetic diversity was high, suggesting nonstraightforward interactive effects of observed and non-observed traits on prey diversity.
The effects of functional and genetic minnow diversity loss on invertebrate (macroinvertebrates and zooplankton) abundance were more consistent than for invertebrate diversity. This suggests again nonstraightforward relationships in this experimental ecosystem, but now between invertebrate diversity and abundance. When using abundance as a proxy for an ecosystem process (which the authors did not), this result illustrates that biodiversity loss in multitrophic communities can have consequences that are challenging to interpret, let alone predict [8,9]. Path analyses showed how the observed changes of invertebrate diversity and abundance co-determined decomposition, a key ecosystem function. These path analyses had highest explanatory power show when including both kinds of intraspecific diversity.
Taken together, the results by Raffard and colleagues suggest that genetic consumer richness can drive species diversity of connected trophic levels and ecosystem processes with similar magnitude as functional diversity. Indeed, the effects of genetic consumer richness were shown to be so strong as to compensate or exacerbate the loss of observed functional richness. The exact mechanisms explaining these effects remain to be identified, however. The possibility that fish grazing by fish with different (observed or not observed) traits regulates coexistence among invertebrate prey, for instance, would depend on how strong fish consumption feeds back on prey growth during a 30-week experiment. As the authors indicate, detailed studies on resource partitioning among consumers (e.g. using stable isotope labelling) can shed light on these matters. Doing so may address a more fundamental question, which is if the mechanisms linking intraspecific diversity to function are different from those linking interspecific diversity to function, and at what time scales.

References

[1] Tilman D, Downing JA (1994) Biodiversity and stability in grasslands. Nature, 367, 363–365. https://doi.org/10.1038/367363a0
[2] Cardinale BJ, Duffy JE, Gonzalez A, Hooper DU, Perrings C, Venail P, Narwani A, Mace GM, Tilman D, Wardle DA, Kinzig AP, Daily GC, Loreau M, Grace JB, Larigauderie A, Srivastava DS, Naeem S (2012) Biodiversity loss and its impact on humanity. Nature, 486, 59–67. https://doi.org/10.1038/nature11148
[3] De Laender F, Rohr JR, Ashauer R, Baird DJ, Berger U, Eisenhauer N, Grimm V, Hommen U, Maltby L, Meliàn CJ, Pomati F, Roessink I, Radchuk V, Brink PJV den (2016) Reintroducing Environmental Change Drivers in Biodiversity–Ecosystem Functioning Research. Trends in Ecology & Evolution, 31, 905–915. https://doi.org/10.1016/j.tree.2016.09.007
[4] Hart SP, Schreiber SJ, Levine JM (2016) How variation between individuals affects species coexistence. Ecology Letters, 19, 825–838. https://doi.org/10.1111/ele.12618
[5] Barabás G, D’Andrea R (2016) The effect of intraspecific variation and heritability on community pattern and robustness. Ecology Letters, 19, 977–986. https://doi.org/10.1111/ele.12636
[6] Raffard A, Cucherousset J, Montoya JM, Richard M, Acoca-Pidolle S, Poésy C, Garreau A, Santoul F, Blanchet S (2020) Intraspecific diversity loss in a predator species alters prey community structure and ecosystem functions. bioRxiv, 2020.06.10.144337, ver. 3 peer-reviewed and recommended by PCI Ecology. https://doi.org/10.1101/2020.06.10.144337
[7] Pásztor L, Botta-Dukát Z, Magyar G, Czárán T, Meszéna G. Theory-Based Ecology: A Darwinian approach. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199577859.001.0001
[8] Binzer A, Guill C, Rall BC, Brose U (2016) Interactive effects of warming, eutrophication and size structure: impacts on biodiversity and food-web structure. Global Change Biology, 22, 220–227. https://doi.org/10.1111/gcb.13086
[9] Schwarz B, Barnes AD, Thakur MP, Brose U, Ciobanu M, Reich PB, Rich RL, Rosenbaum B, Stefanski A, Eisenhauer N (2017) Warming alters energetic structure and function but not resilience of soil food webs. Nature Climate Change, 7, 895–900. https://doi.org/10.1038/s41558-017-0002-z

Barbier et al. (2024) investigated the dynamics of species abundances depending on their ecological niche (abiotic component) and on (numerous) competitive interactions. In line with previous evidence and expectations (Barbier et al. 2018), the authors show that it is possible to robustly infer the mean and variance of interaction coefficients from species co-distributions, while it is not possible to infer the individual coefficient values.

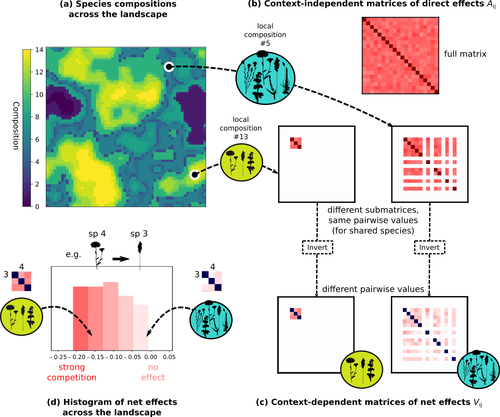
The authors devised a simulation framework representing multispecies dynamics in an heterogeneous environmental context (2D grid landscape). They used a Lotka-Volterra framework involving pairwise interaction coefficients and species-specific carrying capacities. These capacities depend on how well the species niche matches the local environmental conditions, through a Gaussian function of the distance of the species niche centers to the local environmental values.

They considered two contrasted scenarios denoted as « Environmental tracking » and « Dispersal limited ». In the latter case, species are initially seeded over the environmental grid and cannot disperse to other cells, while in the former case they can disperse and possibly be more performant in other cells.

The direct effects of species on one another are encoded in an interaction matrix A, and the authors further considered net interactions depending on the inverse of the matrix of direct interactions (Zelnik et al., 2024). The net effects are context-dependent, i.e., it involves the environment-dependent biotic capacities, even through the interaction terms can be defined between species as independent from local environment.

The results presented here underline that the outcome of many individual competitive interactions can only be understood in terms of macroscopic properties. In essence, the results here echoe the mean field theories that investigate the dynamics of average ecological properties instead of the microscopic components (e.g., McKane et al. 2000). In a philosophical perspective, community ecology has long struggled with analyzing and inferring local determinants of species coexistence from species co-occurrence patterns, so that it was claimed that no universal laws can be derived in the discipline (Lawton 1999). Using different and complementary methods and perspectives, recent research has also shown that species assembly parameter values cannot be unambiguously inferred from species co-occurrences only, even in simple designs where an equilibrium can be reached (Poggiato et al. 2021). Although the roles of high-order competitive interactions and intransivity can lead to species coexistence, the simple view of a single loop of competitive interactions is easily challenged when further interactions and complexity is added (Gallien et al. 2024). But should we put so much emphasis on inferring individual interaction coefficients? In a quest to understand the emerging properties of elementary processes, ecological theory could go forward with a more macroscopic analysis and understanding of species coexistence in many communities.

The authors referred several times to an interesting paper from Schaffer (1981), entitled « Ecological abstraction: the consequences of reduced dimensionality in ecological models ». It proposes that estimating individual species competition coefficients is not possible, but that competition can be assessed at the coarser level of organisation, i.e., between ecological guilds. This idea implies that the dimensionality of the competition equations should be greatly reduced to become tractable in practice. Taking together this claim with the results of the present Barbier et al. (2024) paper, it becomes clearer that the nature of competitive interactions can be addressed through « abstracted » quantities, as those of guilds or the moments of the individual competition coefficients (here the average and the standard deviation).

Therefore the scope of Barbier et al. (2024) framework goes beyond statistical issues in parameter inference, but question the way we must think and represent the numerous competitive interactions in a simplified and robust way.

References

Barbier, Matthieu, Jean-François Arnoldi, Guy Bunin, et Michel Loreau. 2018. « Generic assembly patterns in complex ecological communities ». Proceedings of the National Academy of Sciences 115 (9): 2156‑61. https://doi.org/10.1073/pnas.1710352115
 
Barbier, Matthieu, Guy Bunin, et Mathew A Leibold. 2024. « Getting More by Asking for Less: Linking Species Interactions to Species Co-Distributions in Metacommunities ». bioRxiv, ver. 2 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2023.06.04.543606
 
Gallien, Laure, Maude  Charlie Cavaliere, Marie  Charlotte Grange, François Munoz, et Tamara Münkemüller. 2024. « Intransitive stability collapses under the influence of dominant competitors ». The American Naturalist. https://doi.org/10.1086/730297
 
Lawton, J. H. 1999. « Are There General Laws in Ecology? » Oikos 84 (février):177‑92. https://doi.org/10.2307/3546712
 
McKane, Alan, David Alonso, et Ricard V Solé. 2000. « Mean-field stochastic theory for species-rich assembled communities ». Physical Review E 62 (6): 8466. https://doi.org/10.1103/PhysRevE.62.8466
 
Poggiato, Giovanni, Tamara Münkemüller, Daria Bystrova, Julyan Arbel, James S. Clark, et Wilfried Thuiller. 2021. « On the Interpretations of Joint Modeling in Community Ecology ». Trends in Ecology & Evolution. https://doi.org/10.1016/j.tree.2021.01.002
 
Schaffer, William M. 1981. « Ecological abstraction: the consequences of reduced dimensionality in ecological models ». Ecological monographs 51 (4): 383‑401. https://doi.org/10.2307/2937321
 
Zelnik, Yuval R., Nuria Galiana, Matthieu Barbier, Michel Loreau, Eric Galbraith, et Jean-François Arnoldi. 2024. « How collectively integrated are ecological communities? » Ecology Letters 27 (1): e14358. https://doi.org/10.1111/ele.14358

In this article, Saade et al. (2021) investigate how the rate of local extinctions and their spatial distribution affect recolonization dynamics in metacommunities. They use an elegant combination of microcosm experiments with metacommunities of freshwater ciliates and mathematical modelling mirroring their experimental system. Their main findings are (i) that local patch extinctions increase both local (α-) and inter-patch (β-) diversity in a transient way during the recolonization process, (ii) that these effects depend more on the spatial distribution of extinctions (dispersed or clustered) than on their amount, and (iii) that they may spread regionally.
Microcosm experiments are already quite cool just by themselves and have contributed largely to conceptual advances in community ecology (see Fraser and Keddy 1997, or Jessup et al. 2004 for reviews on this topic), but they are here exploited to a whole further level by the fitting of a metapopulation dynamics model. The model allows both to identify the underlying mechanisms most likely to generate the patterns observed (here, competitive interactions) and to assess the robustness of these patterns when considering larger spatial or temporal scales. This release of experimental limitations allows here for the analysis of quantitative metrics of spatial structure, like the distance to the closest patch, which gives an interesting insight into the functional basis of the effect of the spatial distribution of extinctions.

A major strength of this study is that it highlights the importance of considering the spatial structure explicitly. Recent work on ecological networks has shown repeatedly that network structure affects the propagation of pathogens (Badham and Stocker 2010), invaders (Morel-Journel et al. 2019), or perturbation events (Gilarranz et al. 2017). Here, the spatial structure of the metacommunity is a regular grid of patches, but the distribution of extinction events may be either regularly dispersed (i.e., extinct patches are distributed evenly over the grid and are all surrounded by non-extinct patches only) or clustered (all extinct patches are neighbours). This has a direct effect on the neighbourhood of perturbed patches, and because perturbations have mostly local effects, their recovery dynamics are dominated by the composition of this immediate neighbourhood. In landscapes with dispersed extinctions, the neighbourhood of a perturbed patch is not affected by the amount of extinctions, and neither is its recovery time. In contrast, in landscapes with clustered extinctions, the amount of extinctions affects the depth of the perturbed area, which takes longer to recover when it is larger. Interestingly, the spatial distribution of extinctions here is functionally equivalent to differences in connectivity between perturbed and unperturbed patches, which results in contrasted “rescue recovery” and “mixing recovery” regimes as described by Zelnick et al. (2019).
 
Furthermore, this study focuses on local dynamics of competition and short-term, transient patterns that may have been overlooked by more classical, equilibrium-based approaches of dynamical systems of metacommunities. Indeed, in a metacommunity composed of several competitors, early theoretical work demonstrated that species coexistence is possible at the regional scale only, provided that spatial heterogeneity creates spatial variance in fitness or precludes the superior competitor from accessing certain habitat patches (Skellam 1951, Levins 1969). In the spatially homogeneous experimental system of Saade et al., one of the three ciliate species ends up dominating the community at equilibrium. However, following local, one-time extinction events, the community endures a recolonization process in which differences in dispersal may provide temporary spatial niches for inferior competitors. These transient patterns might prove essential to understand and anticipate the resilience of natural systems that are under increasing pressure, and enduring ever more frequent and intense perturbations (IPBES 2019). Spatial autocorrelation in extinction events was previously identified as a risk for stability and persistence of metacommunities (Ruokolainen 2013, Kahilainen et al. 2018). These new results show that autocorrelated perturbations also have longer-lasting effects, which is likely to increase their overall impact on metacommunity dynamics. As spatial and temporal autocorrelation of temperature and extreme climatic events are expected to increase (Di Cecco and Gouthier 2018), studies that investigate how metacommunities respond to the structure of the distribution of perturbations are more necessary than ever.
 
References

Badham J, Stocker R (2010) The impact of network clustering and assortativity on epidemic behaviour. Theoretical Population Biology, 77, 71–75. https://doi.org/10.1016/j.tpb.2009.11.003
 
Di Cecco GJ, Gouhier TC (2018) Increased spatial and temporal autocorrelation of temperature under climate change. Scientific Reports, 8, 14850. https://doi.org/10.1038/s41598-018-33217-0
 
Fraser LH, Keddy P (1997) The role of experimental microcosms in ecological research. Trends in Ecology & Evolution, 12, 478–481. https://doi.org/10.1016/S0169-5347(97)01220-2
 
Gilarranz LJ, Rayfield B, Liñán-Cembrano G, Bascompte J, Gonzalez A (2017) Effects of network modularity on the spread of perturbation impact in experimental metapopulations. Science, 357, 199–201. https://doi.org/10.1126/science.aal4122
 
IPBES (2019) Summary for policymakers of the global assessment report on biodiversity and ecosystem services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services. S. Díaz, J. Settele, E. S. Brondízio E.S., H. T. Ngo, M. Guèze, J. Agard, A. Arneth, P. Balvanera, K. A. Brauman, S. H. M. Butchart, K. M. A. Chan, L. A. Garibaldi, K. Ichii, J. Liu, S. M. Subramanian, G. F. Midgley, P. Miloslavich, Z. Molnár, D. Obura, A. Pfaff, S. Polasky, A. Purvis, J. Razzaque, B. Reyers, R. Roy Chowdhury, Y. J. Shin, I. J. Visseren-Hamakers, K. J. Willis, and C. N. Zayas (eds.). IPBES secretariat, Bonn, Germany. 56 pages. https://doi.org/10.5281/zenodo.3553579 
 
Jessup CM, Kassen R, Forde SE, Kerr B, Buckling A, Rainey PB, Bohannan BJM (2004) Big questions, small worlds: microbial model systems in ecology. Trends in Ecology & Evolution, 19, 189–197. https://doi.org/10.1016/j.tree.2004.01.008
 
Kahilainen A, van Nouhuys S, Schulz T, Saastamoinen M (2018) Metapopulation dynamics in a changing climate: Increasing spatial synchrony in weather conditions drives metapopulation synchrony of a butterfly inhabiting a fragmented landscape. Global Change Biology, 24, 4316–4329. https://doi.org/10.1111/gcb.14280

Levins R (1969) Some Demographic and Genetic Consequences of Environmental Heterogeneity for Biological Control1. Bulletin of the Entomological Society of America, 15, 237–240. https://doi.org/10.1093/besa/15.3.237
 
Morel-Journel T, Assa CR, Mailleret L, Vercken E (2019) Its all about connections: hubs and invasion in habitat networks. Ecology Letters, 22, 313–321. https://doi.org/10.1111/ele.13192

Ruokolainen L (2013) Spatio-Temporal Environmental Correlation and Population Variability in Simple Metacommunities. PLOS ONE, 8, e72325. https://doi.org/10.1371/journal.pone.0072325

Saade C, Kefi S, Gougat-Barbera C, Rosenbaum B, Fronhofer EA (2021) Spatial distribution of local patch extinctions drives recovery dynamics in metacommunities. bioRxiv, 2020.12.03.409524, ver. 4 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2020.12.03.409524
 
Skellam JG (1951) Random Dispersal in Theoretical Populations. Biometrika, 38, 196–218. https://doi.org/10.2307/2332328
 
Zelnik YR, Arnoldi J-F, Loreau M (2019) The three regimes of spatial recovery. Ecology, 100, e02586. https://doi.org/10.1002/ecy.2586