MASSOL Francois
- UMR 7618 IEES, CNRS, Paris, France
- Community ecology, Dispersal & Migration, Evolutionary ecology, Food webs, Interaction networks, Spatial ecology, Metacommunities & Metapopulations, Theoretical ecology
- recommender, manager, administrator
Recommendations: 2
Reviews: 2
Recommendations: 2

InsectChange: Comment
Why we need to clean the Augean stables of ecology – the case of InsectChange
Recommended by Francois Massol based on reviews by Bradley Cardinale and 1 anonymous reviewerAs biodiversity has become a major global concern for a variety of stakeholders, and society in general, assessments of biodiversity trends at all spatial scales have flourished in the past decades. To assess trends, one needs data, and the more precise the data, the more precise the trend. Or, if precision is not perfect, uncertainty in the data must be acknowledged and accounted for. Such considerations have already been raised in ecology, most notably regarding the value of species distribution data to model the current and future distribution of species (Rocchini et al., 2011, Duputié et al., 2014, Tessarolo et al., 2021), leading to serious doubts regarding the value of public databases (Maldonado et al., 2015). And more recently similar issues have been raised regarding databases of species traits (Augustine et al., 2024), emphasizing the importance of good data practice and traceability.
Science is by nature a self-correcting human process, with many steps of the scientific activity prone to errors and misinterpretations. Collation of ecological data, sadly, is proof of this. Spurred by the astonishing results of Hallmann et al. (2017) regarding the decline of insect biomass, and to more precisely answer the question of biodiversity trends in insects and settle an ongoing debate (Cardinale et al., 2018), van Klink et al. (2020, 2021) established the InsectChange database. Several perceptive comments have already been made regarding the possible issues in the methods and interpretations of this study (Desquilbet et al., 2020, Jähnig et al., 2021, Duchenne et al., 2022). However, the biggest issue might have been finally unearthed by Gaume & Desquilbet (2024): with poorly curated data, the InsectChange database is unlikely to support most of the initial claims regarding insect biodiversity trends.
The compilation of errors and inconsistencies present in InsectChange and evinced by Gaume & Desquilbet (2024) is stunning to say the least, with a mix of field and experimental data combined without regard for experimental manipulation of environmental factors, non-standardised transformations of abundances, the use of non-insect taxa to compute insect trends, and inadequate geographical localizations of samplings. I strongly advise all colleagues interested in the study of biodiversity from global databases to consider the points raised by the authors, as it is quite likely that other databases might suffer from the same ailments as well. Reading this paper is also educating and humbling in its own way, since the publication of the original papers based on InsectChange seems to have proceeded without red flags from reviewers or editors. The need for publishing fast results that will make the next buzz, thus obeying the natural selection of bad science (Smaldino and McElreath, 2016), might be the systemic culprit. However, this might also be the opportunity ecology needs to consider the reviewing and curation of data as a crucial step of science quality assessment. To make final assessments, let us proceed with less haste.
References
Augustine, S. P., Bailey-Marren, I., Charton, K. T., Kiel, N. G. & Peyton, M. S. (2024) Improper data practices erode the quality of global ecological databases and impede the progress of ecological research. Global Change Biology, 30, e17116. https://doi.org/10.1111/gcb.17116
Cardinale, B. J., Gonzalez, A., Allington, G. R. H. & Loreau, M. (2018) Is local biodiversity declining or not? A summary of the debate over analysis of species richness time trends. Biological Conservation, 219, 175-183. https://doi.org/10.1016/j.biocon.2017.12.021
Desquilbet, M., Gaume, L., Grippa, M., Céréghino, R., Humbert, J.-F., Bonmatin, J.-M., Cornillon, P.-A., Maes, D., Van Dyck, H. & Goulson, D. (2020) Comment on “Meta-analysis reveals declines in terrestrial but increases in freshwater insect abundances”. Science, 370, eabd8947. https://doi.org/10.1126/science.abd8947
Duchenne, F., Porcher, E., Mihoub, J.-B., Loïs, G. & Fontaine, C. (2022) Controversy over the decline of arthropods: a matter of temporal baseline? Peer Community Journal, 2. https://doi.org/10.24072/pcjournal.131
Duputié, A., Zimmermann, N. E. & Chuine, I. (2014) Where are the wild things? Why we need better data on species distribution. Global Ecology and Biogeography, 23, 457-467. https://doi.org/10.1111/geb.12118
Gaume, L. & Desquilbet, M. (2024) InsectChange: Comment. biorXiv, ver.4 peer-reviewed and recommended by PCI Ecology https://doi.org/10.1101/2023.06.17.545310
Hallmann, C. A., Sorg, M., Jongejans, E., Siepel, H., Hofland, N., Schwan, H., Stenmans, W., Müller, A., Sumser, H., Hörren, T., Goulson, D. & de Kroon, H. (2017) More than 75 percent decline over 27 years in total flying insect biomass in protected areas. PLOS ONE, 12, e0185809. https://doi.org/10.1371/journal.pone.0185809
Jähnig, S. C., Baranov, V., Altermatt, F., Cranston, P., Friedrichs-Manthey, M., Geist, J., He, F., Heino, J., Hering, D., Hölker, F., Jourdan, J., Kalinkat, G., Kiesel, J., Leese, F., Maasri, A., Monaghan, M. T., Schäfer, R. B., Tockner, K., Tonkin, J. D. & Domisch, S. (2021) Revisiting global trends in freshwater insect biodiversity. WIREs Water, 8, e1506. https://doi.org/10.1002/wat2.1506
Maldonado, C., Molina, C. I., Zizka, A., Persson, C., Taylor, C. M., Albán, J., Chilquillo, E., Rønsted, N. & Antonelli, A. (2015) Estimating species diversity and distribution in the era of Big Data: to what extent can we trust public databases? Global Ecology and Biogeography, 24, 973-984. https://doi.org/10.1111/geb.12326
Rocchini, D., Hortal, J., Lengyel, S., Lobo, J. M., Jiménez-Valverde, A., Ricotta, C., Bacaro, G. & Chiarucci, A. (2011) Accounting for uncertainty when mapping species distributions: The need for maps of ignorance. Progress in Physical Geography, 35, 211-226. https://doi.org/10.1177/0309133311399491
Smaldino, P. E. & McElreath, R. (2016) The natural selection of bad science. Royal Society Open Science, 3. https://doi.org/10.1098/rsos.160384
Tessarolo, G., Ladle, R. J., Lobo, J. M., Rangel, T. F. & Hortal, J. (2021) Using maps of biogeographical ignorance to reveal the uncertainty in distributional data hidden in species distribution models. Ecography, 44, 1743-1755. https://doi.org/10.1111/ecog.05793
van Klink, R., Bowler, D. E., Comay, O., Driessen, M. M., Ernest, S. K. M., Gentile, A., Gilbert, F., Gongalsky, K. B., Owen, J., Pe'er, G., Pe'er, I., Resh, V. H., Rochlin, I., Schuch, S., Swengel, A. B., Swengel, S. R., Valone, T. J., Vermeulen, R., Wepprich, T., Wiedmann, J. L. & Chase, J. M. (2021) InsectChange: a global database of temporal changes in insect and arachnid assemblages. Ecology, 102, e03354. https://doi.org/10.1002/ecy.3354
van Klink, R., Bowler, D. E., Gongalsky, K. B., Swengel, A. B., Gentile, A. & Chase, J. M. (2020) Meta-analysis reveals declines in terrestrial but increases in freshwater insect abundances. Science, 368, 417-420. https://doi.org/10.1126/science.aax9931

Pathogen community composition and co-infection patterns in a wild community of rodents
Reservoirs of pestilence: what pathogen and rodent community analyses can tell us about transmission risk
Recommended by Francois Massol based on reviews by Adrian Diaz, Romain Pigeault and 1 anonymous reviewerRodents are well known as one of the main animal groups responsible for human-transmitted pathogens. As such, it seems logical to try and survey what kinds of pathogenic microbes might be harboured by wild rodents, in order to establish some baseline surveillance and prevent future zoonotic outbreaks (Bernstein et al., 2022). This is exactly what Abbate et al. (2023) endeavoured and their findings are intimidating. Based on quite a large sampling effort, they collected more than 700 rodents of seven species around two villages in northeastern France. They looked for molecular markers indicative of viral and bacterial infections and proceeded to analyze their pathogen communities using multivariate techniques.
Variation in the prevalence of the different pathogens was found among host species, with e.g. signs of CPXV more prevalent in Cricetidae while some Mycoplasma strains were more prevalent in Muridae. Co-circulation of pathogens was found in all species, with some evidencing signs of up to 12 different pathogen taxa. The diversity of co-circulating pathogens was markedly different between host species and higher in adult hosts, but not affected by sex. The dataset also evinced some slight differences between habitats, with meadows harbouring a little more diversity of rodent pathogens than forests. Less intuitively, some pathogen associations seemed quite repeatable, such as the positive association of Bartonella spp. with CPXV in the montane water vole. The study allowed the authors to test several associations already described in the literature, including associations between different hemotropic Mycoplasma species.
I strongly invite colleagues interested in zoonoses, emerging pandemics and more generally One Health to read the paper of Abbate et al. (2023) and try to replicate them across the world. To prevent the next sanitary crises, monitoring rodents, and more generally vertebrates, population demographics is a necessary and enlightening step (Johnson et al., 2020), but insufficient. Following the lead of colleagues working on rodent ectoparasites (Krasnov et al., 2014), we need more surveys like the one described by Abbate et al. (2023) to understand the importance of the dilution effect in the prevalence and transmission of microbial pathogens (Andreazzi et al., 2023) and the formation of epidemics. We also need other similar studies to assess the potential of different rodent species to carry pathogens more or less capable of infecting other mammalian species (Morand et al., 2015), in other places in the world.
References
Abbate, J. L., Galan, M., Razzauti, M., Sironen, T., Voutilainen, L., Henttonen, H., Gasqui, P., Cosson, J.-F. & Charbonnel, N. (2023) Pathogen community composition and co-infection patterns in a wild community of rodents. BioRxiv, ver.4 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2020.02.09.940494
Andreazzi, C. S., Martinez-Vaquero, L. A., Winck, G. R., Cardoso, T. S., Teixeira, B. R., Xavier, S. C. C., Gentile, R., Jansen, A. M. & D'Andrea, P. S. (2023) Vegetation cover and biodiversity reduce parasite infection in wild hosts across ecological levels and scales. Ecography, 2023, e06579.
https://doi.org/10.1111/ecog.06579
Bernstein, A. S., Ando, A. W., Loch-Temzelides, T., Vale, M. M., Li, B. V., Li, H., Busch, J., Chapman, C. A., Kinnaird, M., Nowak, K., Castro, M. C., Zambrana-Torrelio, C., Ahumada, J. A., Xiao, L., Roehrdanz, P., Kaufman, L., Hannah, L., Daszak, P., Pimm, S. L. & Dobson, A. P. (2022) The costs and benefits of primary prevention of zoonotic pandemics. Science Advances, 8, eabl4183.
https://doi.org/10.1126/sciadv.abl4183
Johnson, C. K., Hitchens, P. L., Pandit, P. S., Rushmore, J., Evans, T. S., Young, C. C. W. & Doyle, M. M. (2020) Global shifts in mammalian population trends reveal key predictors of virus spillover risk. Proceedings of the Royal Society B: Biological Sciences, 287, 20192736.
https://doi.org/10.1098/rspb.2019.2736
Krasnov, B. R., Pilosof, S., Stanko, M., Morand, S., Korallo-Vinarskaya, N. P., Vinarski, M. V. & Poulin, R. (2014) Co-occurrence and phylogenetic distance in communities of mammalian ectoparasites: limiting similarity versus environmental filtering. Oikos, 123, 63-70.
https://doi.org/10.1111/j.1600-0706.2013.00646.x
Morand, S., Bordes, F., Chen, H.-W., Claude, J., Cosson, J.-F., Galan, M., Czirjak, G. Á., Greenwood, A. D., Latinne, A., Michaux, J. & Ribas, A. (2015) Global parasite and Rattus rodent invasions: The consequences for rodent-borne diseases. Integrative Zoology, 10, 409-423.
https://doi.org/10.1111/1749-4877.12143
Reviews: 2
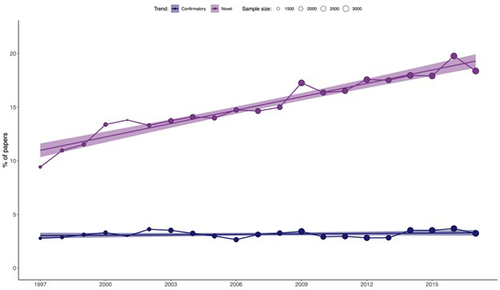
On the quest for novelty in ecology
From Paradigm to Publication: What Does the Pursuit of Novelty Reveal in Ecology?
Recommended by François Munoz based on reviews by Francois Massol, Matthias Grenié and 1 anonymous reviewerIn this study, Ottaviani et al. (2025) examined the variation in the use of terms related to "novelty" in 52,236 abstracts published between 1997 and 2017 across 17 ecological journals. They also analyzed the change in the frequency of terms related to "confirmatory" results. Their findings revealed a clear and consistent increase in the use of "novelty" terms, while the frequency of "confirmatory" terms remained relatively stable. This trend was observed across all the ecological journals, with the exception of Austral Ecology. Furthermore, the greater use of "novelty" terms was correlated with higher citation counts and publication in journals with higher impact factors. These findings should prompt further reflection on our research practices and may be connected to ongoing discussions in the philosophy of science.
Thomas S. Kuhn's seminal work, The Structure of Scientific Revolutions (1962), challenged traditional views of scientific progress. Central to Kuhn's argument is the idea that science progresses through periods of adherence to a dominant "paradigm"—a framework that provides scientists with puzzles to solve and the tools to solve them. A scientific crisis arises when the paradigm fails to address emerging anomalies, leading to the replacement of the old paradigm with a new one, a process Kuhn calls a "scientific revolution." Kuhn's perspective stands in stark contrast to previous views, which held that science progresses through the steady accumulation of truths or the gradual refinement of theories, often guided by the scientific method. One might wonder if the growing emphasis on "novelty" in ecological research mirrors the idea that theories are gradually refined until an exceptional discovery sparks a paradigm shift. In ecology, such a shift could be seen in the transition from niche-based theories of biodiversity dynamics (1960s-2000) to the radical neutral theory (Hubbell, 2001), which posits that diverse ecosystems can exist without niche differences. This paradigm was initially met with fierce opposition but eventually led to more integrative theories, recognizing the combined influence of both niche-based and neutral processes (Gravel et al., 2006, among others).
What, then, is the current paradigm in ecology? Kuhn's theory of scientific progress suggests alternating periods of "normal" and "revolutionary" science. Normal science is characterized by cumulative puzzle-solving within established frameworks, while revolutionary science involves major shifts that can invalidate previous knowledge, a phenomenon Kuhn terms "Kuhn-loss." Kuhn rejected both the traditional and Popperian views on scientific revolutions. He argued that normal science depends on a shared commitment to certain beliefs, values, methods, and even metaphysical assumptions, which he referred to as a "disciplinary matrix" or "paradigm." This collective commitment is essential for scientific progress and must be instilled during the training of scientists. Kuhn's emphasis on the conservative nature of normal science contrasts with the heroic idea of continuous innovation and Popper's view of scientists constantly seeking to falsify theories. However, contemporary ecological research often follows the hypothetico-deductive approach championed by Popper. In light of these contrasting views, one might ask: What is the status of "novelty" in modern ecology? Is it contributing to the gradual solving of scientific puzzles, or is it focused on refuting hypotheses? Should "novelty" and "confirmatory" research be seen as opposites, or should both contribute to the advancement of science? Finally, is the increasing use of "novelty" terms a precursor to a scientific revolution, as Kuhn defined it, or merely a semantic trend driven by editorial policies aimed at attracting readers rather than contributing to real scientific progress?
In conclusion, Ottaviani's study provides compelling evidence of the growing use of "novelty" terms in ecological journals, but it remains unclear whether this trend signals the onset of a Kuhnian "scientific revolution." This work should spark further discussion on the nature of current research practices, which may either facilitate or hinder the emergence of new paradigms.
References
Gravel, D., Canham, C. D., Beaudet, M., & Messier, C. (2006). Reconciling niche and neutrality: the continuum hypothesis. Ecology letters, 9(4), 399-409. https://doi.org/10.1111/j.1461-0248.2006.00884.x
Hubbell, S. P. (2001). The Unified Neutral Theory of Biodiversity and Biogeography, vol.1, Princeton and Oxford: Princeton University Press.
Kuhn, T. S. (1962). The structure of scientific revolutions. International Encyclopedia of Unified Science, vol.2, 1962.
Ottaviani, G., Martinez, A., Petit Bon, M., Mammola, S. (2025). On the quest for novelty in ecology. bioRxiv, ver.4 peer-reviewed and recommended by PCI Ecology. https://doi.org/10.1101/2023.02.27.530333
Beating your neighbor to the berry patch
When more competitors means less harvested resource
Recommended by François Munoz based on reviews by Francois Massol, Jeremy Van Cleve and 1 anonymous reviewerIn this paper, Alan R. Rogers (2021) examines the dynamics of foraging strategies for a resource that gains value over time (e.g., ripening fruits), while there is a fixed cost of attempting to forage the resource, and once the resource is harvested nothing is left for other harvesters. For this model, not any pure foraging strategy is evolutionary stable. A mixed equilibrium exists, i.e., with a mixture of foraging strategies within the population, which is still evolutionarily unstable. Nonetheless, Alan R. Rogers shows that for a large number of competitors and/or high harvesting cost, the mixture of strategies remains close to the mixed equilibrium when simulating the dynamics. Surprisingly, in a large population individuals will less often attempt to forage the resource and will instead “go fishing”. The paper also exposes an experiment of the game with students, which resulted in a strategy distribution somehow close to the theoretical mixture of strategies.
The economist John F. Nash Jr. (1950) gained the Nobel Prize of economy in 1994 for his game theoretical contributions. He gave his name to the “Nash equilibrium”, which represents a set of individual strategies that is reached whenever all the players have nothing to gain by changing their strategy while the strategies of others are unchanged. Alan R. Rogers shows that the mixed equilibrium in the foraging game is such a Nash equilibrium. Yet it is evolutionarily unstable insofar as a distribution close to the equilibrium can invade.
The insights of the study are twofold. First, it sheds light on the significance of Nash equilibrium in an ecological context of foraging strategies. Second, it shows that an evolutionarily unstable state can rule the composition of the ecological system. Therefore, the contribution made by the paper should be most significant to better understand the dynamics of competitive communities and their eco-evolutionary trajectories.
References
Nash JF (1950) Equilibrium points in n-person games. Proceedings of the National Academy of Sciences, 36, 48–49. https://doi.org/10.1073/pnas.36.1.48
Rogers AR (2021) Beating your Neighbor to the Berry Patch. bioRxiv, 2020.11.12.380311, ver. 8 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2020.11.12.380311