
BEREC Ludek
- Institute of Entomology, Laboratory of Theoretical Ecology, Biology Centre of the Czech Academy of Sciences, Ceske Budejovice, Czech Republic
- Eco-evolutionary dynamics, Epidemiology, Population ecology, Theoretical ecology
- recommender
Recommendations: 0
Reviews: 2
Reviews: 2
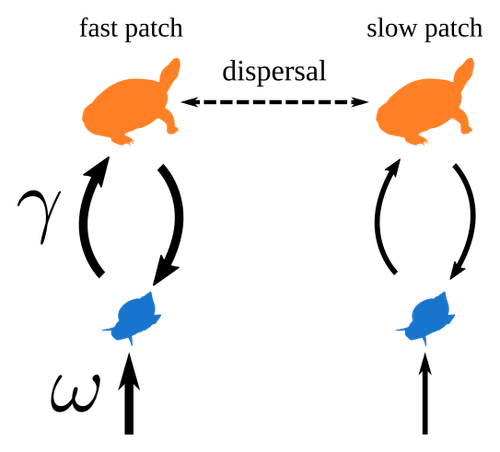
Spatial heterogeneity of interaction strength has contrasting effects on synchrony and stability in trophic metacommunities
How does spatial heterogeneity affect stability of trophic metacommunities?
Recommended by Werner Ulrich based on reviews by Phillip P.A. Staniczenko, Ludek Berec and Diogo ProveteThe temporal or spatial variability in species population sizes and interaction strength of animal and plant communities has a strong impact on aggregate community properties (for instance biomass), community composition, and species richness (Kokkoris et al. 2002). Early work on spatial and temporal variability strongly indicated that asynchronous population and environmental fluctuations tend to stabilise community structures and diversity (e.g. Holt 1984, Tilman and Pacala 1993, McCann et al. 1998, Amarasekare and Nisbet 2001). Similarly, trophic networks might be stabilised by spatial heterogeneity (Hastings 1977) and an asymmetry of energy flows along food chains (Rooney et al. 2006). The interplay between temporal, spatial, and trophic heterogeneity within the meta-community concept has got much less interest. In the recent preprint in PCI Ecology, Quévreux et al. (2023) report that Spatial heterogeneity of interaction strength has contrasting effects on synchrony and stability in trophic metacommunities. These authors rightly notice that the interplay between trophic and spatial heterogeneity might induce contrasting effects depending on the internal dynamics of the system. Their contribution builds on prior work (Quévreux et al. 2021a, b) on perturbed trophic cascades.
I found this paper particularly interesting because it is in the, now century-old, tradition to show that ecological things are not so easy. Since the 1930th, when Nicholson and Baily and others demonstrated that simple deterministic population models might generate stability and (pseudo-)chaos ecologists have realised that systems triggered by two or more independent processes might be intrinsically unpredictable and generate different outputs depending on the initial parameter settings. This resembles the three-body problem in physics. The present contribution of Quévreux et al. (2023) extends this knowledge to an example of a spatially explicit trophic model. Their main take-home message is that asymmetric energy flows in predator–prey relationships might have contrasting effects on the stability of metacommunities receiving localised perturbations. Stability is context dependent.
Of course, the work is merely a theoretical exercise using a simplistic trophic model. It demands verification with field data. Nevertheless, we might expect even stronger unpredictability in more realistic multitrophic situations. Therefore, it should be seen as a proof of concept. Remember that increasing trophic connectance tends to destabilise food webs (May 1972). In this respect, I found the final outlook to bioconservation ambitious but substantiated. Biodiversity management needs a holistic approach focusing on all aspects of ecological functioning. I would add the need to see stability and biodiversity within an evolutionary perspective.
References
Amarasekare P, Nisbet RM (2001) Spatial Heterogeneity, Source‐Sink Dynamics, and the Local Coexistence of Competing Species. The American Naturalist, 158, 572–584. https://doi.org/10.1086/323586
Hastings A (1977) Spatial heterogeneity and the stability of predator-prey systems. Theoretical Population Biology, 12, 37–48. https://doi.org/10.1016/0040-5809(77)90034-X
Holt RD (1984) Spatial Heterogeneity, Indirect Interactions, and the Coexistence of Prey Species. The American Naturalist, 124, 377–406. https://doi.org/10.1086/284280
Kokkoris GD, Jansen VAA, Loreau M, Troumbis AY (2002) Variability in interaction strength and implications for biodiversity. Journal of Animal Ecology, 71, 362–371. https://doi.org/10.1046/j.1365-2656.2002.00604.x
May RM (1972) Will a Large Complex System be Stable? Nature, 238, 413–414. https://doi.org/10.1038/238413a0
McCann K, Hastings A, Huxel GR (1998) Weak trophic interactions and the balance of nature. Nature, 395, 794–798. https://doi.org/10.1038/27427
Quévreux P, Barbier M, Loreau M (2021) Synchrony and Perturbation Transmission in Trophic Metacommunities. The American Naturalist, 197, E188–E203. https://doi.org/10.1086/714131
Quévreux P, Pigeault R, Loreau M (2021) Predator avoidance and foraging for food shape synchrony and response to perturbations in trophic metacommunities. Journal of Theoretical Biology, 528, 110836. https://doi.org/10.1016/j.jtbi.2021.110836
Quévreux P, Haegeman B, Loreau M (2023) Spatial heterogeneity of interaction strength has contrasting effects on synchrony and stability in trophic metacommunities. hal-03829838, ver. 2 peer-reviewed and recommended by Peer Community in Ecology. https://hal.science/hal-03829838
Rooney N, McCann K, Gellner G, Moore JC (2006) Structural asymmetry and the stability of diverse food webs. Nature, 442, 265–269. https://doi.org/10.1038/nature04887
Tilman D, Pacala S (1993) The maintenance of species richness in plant communities. In: Ricklefs, R.E., Schluter, D. (eds) Species Diversity in Ecological Communities: Historical and Geographical Perspectives. University of Chicago Press, pp. 13–25.

A macro-ecological approach to predators' functional response
A meta-analysis to infer generic predator functional response
Recommended by Samir Simon Suweis based on reviews by Ludek Berec and gyorgy barabasSpecies interactions are classically derived from the law of mass action: the probability that, for example, a predation event occurs is proportional to the product of the density of the prey and predator species. In order to describe how predator and prey species populations grow, is then necessary to introduce functional response, describing the intake rate of a consumer as a function of food (e.g. prey) density.
Linear functional responses shapes are typically introduced in the ecological modeling of population dynamics for both predator-prey and mutualistic systems [1,2]. Recently some works have proposed alternatives to the classic approach for mutualistic systems [3,4], both because cooperative interactions also model effect not directly related to mass action [3] and for analytical tractability [4,5].
In this work [6] the authors challenge the classic modeling of functional response also for predator-prey systems. In particular, they use a meta-analysis of several observational studies of predator-prey ecosystems to infer a generic predator functional response, fitting a phenomenological generalization of the mass-action law. Using advanced statistical analysis, they show that the functional response obtained from data is clearly different from the mass-action assumption. In fact, they found that it scales sub-linearly as the square root of the ratio between predator and prey biomass. They further argue that, from a macro-ecological point of view, using such a phenomenological relationship might be more valuable than relying on various mechanistic functional response formulations.
The manuscript thus provides an interesting different perspective on how to approach predator-prey modelling and for this reason, I have recommended the work for PCI Ecology.
References
[1] Volterra, V. (1928). Variations and Fluctuations of the Number of Individuals in Animal Species living together. ICES Journal of Marine Science, 3(1), 3–51. doi: 10.1093/icesjms/3.1.3
[2] Bastolla, U., Fortuna, M. A., Pascual-García, A., Ferrera, A., Luque, B., and Bascompte, J. (2009). The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature, 458(7241), 1018–1020. doi: 10.1038/nature07950
[3] Tu, C., Suweis, S., Grilli, J., Formentin, M., and Maritan, A. (2019). Reconciling cooperation, biodiversity and stability in complex ecological communities. Scientific Reports, 9(1), 1–10. doi: 10.1038/s41598-019-41614-2
[4] García-Algarra, J., Galeano, J., Pastor, J. M., Iriondo, J. M., and Ramasco, J. J. (2014). Rethinking the logistic approach for population dynamics of mutualistic interactions. Journal of Theoretical Biology, 363, 332–343. doi: 10.1016/j.jtbi.2014.08.039
[5] Suweis, S., Simini, F., Banavar, J. R., and Maritan, A. (2013). Emergence of structural and dynamical properties of ecological mutualistic networks. Nature, 500(7463), 449–452. doi: 10.1038/nature12438
[6] Barbier, M., Wojcik, L., and Loreau, M. (2020). A macro-ecological approach to predators’ functional response. BioRxiv, 832220, ver. 4 recommended and peer-reviewed by Peer Community in Ecology. doi: 10.1101/832220