The authors have successfully addressed all of my comments and I believe that the manuscript is improved in both content and readability. I am happy for the manscript to be accepted in this state.

The changes the authors make have greatly improved the manuscript.  The extra information and clarification they provide address all of my comments.  However, the additional information they provide about equations 1 and 2 make it clear that the model formulation must be remedied before publication.  This will require rerunning simulations, etc. since the model will need to be refit following reformulation.  As it is written, unfortunately the model is not mathematically well defined, leading to potentially incoherent situations.  For example, if you want to simulate data for a population in which prevalence is equal to 0, but simultaneously all members of the population have a covariate value that is known to perfectly correlate with disease, then you have a problem.  The prevalence parameter implies all y_i should equal 0, while the covariate implies all y_i should be equal to 1.  The model needs to avoid such mathematically pathological situations, and it is unreasonable to simply advise against use in such scenarios in a discussion section for more substantial reasons described below.

Standard probability rules require a random variable to have a single definition.  Defining it twice, as the authors do via equations 1 and 2 is not a valid way to specify a joint probability model.  The authors may only specify a single Bernoulli distribution for y_i.  The authors must explicitly write mathematically, in an equation, how they wish the individual-level covariates to interact or otherwise relate to population-level prevalence.  Although it is simple to write a single equation involving both theta and the covariates, the revision could potentially place the population-level prevalence term in tension with the effect of individual level covariates.  Naturally, population-level prevalence partly arises from the aggregate effects of individual-level risks and outcomes.  A revision will likely require some careful thinking about how to (re?)interpret model parameters.

Statistical software may or may not enforce the one definition rule, but that does not justify ignoring it.  For example, while the R software Stan may interpret multiple definitions for a random variable as a user’s request to make two separate contributions for the variable to the log-likelihood, the R software Nimble refuses to build models when variables are defined twice.  In general, statistical software is not necessarily provided with guard rails to prevent users from doing “prohibited” things.  Drawing on an example commonly taught in introductory regression modeling classes, the R function lm() (and equivalent functions in other statistical software, like SASS) will let users fit a least squares linear regression model to binary data, even though users should use logistic regression models (or similar) to fit binary data.  When software provides estimates for models that are not mathematically well defined, the estimates in general will not be able to be interpreted in the way users intend.  Software predictions may also be non-sensible, which is the main concern with fitting binary data to a least square linear regression.

This study describes a new computational approach for obtaining viral prevalence estimates using naturally pooled samples, the use of which is currently limited to presence/absence information in an area.

The methods presented represent a significant advance in the analysis of pooled samples and have the potential to allow the study of pathogen prevalence in wildlife populations without the time, expense, and hazard of catching and handling individual animals. Where individual level samples are also available, the authors include methods for directly incorporating individual covariates. The true prevalence over time section of the model offers the potential to, although not explored by the authors, directly incorporate a transmission model and fit these parameters which should allow for the direct combining of uncertainty from the other sections of the model. The discussion provides a fair assessment of the potential utility of the model whilst discussing its limitations, specific requirements, and drawbacks.

Whilst the authors explore a good range of non-ideal data scenarios, I am not convinced that these scenarios reflect a ‘realistic’ dataset. I would like to see if the close match to the simulated prevalence is maintained when multiple potentially confounding factors are combined, i.e., small and varying sample sizes, taken at irregular intervals. I would recommend not overstating the realism of the test data in the discussion.

Below are some suggestions for clarifications of the text and figures.

I’m not sure of the length allowances for the abstract in this journal, but I find the abstract rather long, which detracts rather than enhances interest in the article.

The introduction describes in detail the current state of the field, and the need for the model. The research question is clearly presented but could again be more concise for readability.

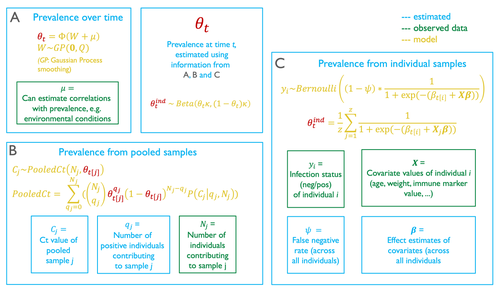
Figure 1 – The black lines on the figure showing the connectivity between the sections aren’t very informative and I think make things less clear. That the relevant parameter is highlighted in a different colour is enough to see that it occurs in all three sections. Perhaps make it bold as well if the colour alone is not clear enough. Is θ observed as per the key? Is that not what all sections of the model come together to estimate? If the important thing is that it’s estimated by all of them, put it outside of the other boxes.

Should equation 2 match the relevant equation in figure 1 (currently the yellow equation in box C)?

Page 10 line 5 – the three key factors that influence final pooled concentration. You mention a few paragraphs later than urine volume is assumed to be equal, but on first read-through I was wondering in this section why it was being ignored. A simple line of ‘here we focus on these first two factors’ would do to make readers stop wondering where the third one was!

Where laboratory experiments are required to determine distributions/baseline values should be clarified.

Add to the discussion on pool size limitations of this method that this should be taken into account during the field experimental design and set-up if feasible for most reliable results. Possibly mention that this is more suitable for some wildlife species than others given their usual behaviours and living arrangements.

Figure 2 – Would add either in the figure or the legend, how these steps (A-D) relate to the numbered steps in the main text. Am I understanding correctly that example in this figure (Ct 36, 2/3 bats/ 20% prevalence) is randomly chosen, and that this process would need to be completed for all possible combinations? If so, add a final line in the legend stating this?

Figure 4 – I think that the 50% CI shading should stand out a bit more. I would also recommend moving the datapoints to the top layer of the figure so that they are not hidden behind the fitted prevalence curves or the credible interval band.