

Understanding the effects of environmental perturbations on coexistence is a key challenge in ecology, and models have played an important role in structuring our ideas and generating predictions, leading to quantitative hypotheses. In such models, environmental perturbations are often captured by changes in parameter values, such as the intrinsic growth rates of species (1–3). The question then becomes how much one can change these parameters without breaking coexistence and thus losing species (4).
An intuitively appealing approach to address this question is to calculate a model’s feasibility domain (5–7). Loosely defined, it is the fraction of parameter settings leading to the coexistence of all species. Mathematically speaking, it is a high-dimensional triangle, of which one can calculate the size, just as for plain two-dimensional triangles. Parameter settings outside of this triangle break coexistence. Thus, it seems logical that greater feasibility domains would make for more robust ecosystems. However, careful interpretation is key: a greater feasibility domain merely implies that across many attempts at running a model with different random parameter settings, coexistence will be more frequent. It does not necessarily inform us how much one can perturb the parameters of a community with a predefined parameter setting. To get this information, we also need to know the shape of the triangle (7): perturbations more easily knock the parameter setting out of a flat triangle than out of an equilateral triangle.
Desaillais et al. (8) develop a new theory that sheds light on what drives the shape of the feasibility domain. Specifically, they present the probability distribution that tells how close to the edge of the feasibility domain the parameter settings in that domain tend to be. For example, all points in a very flat triangle are close to its edge, while in an equilateral triangle, most points are safely stowed inside. The results show how, in a Lotka-Volterra model, the matrix of species interactions fully defines this distribution, which makes the technique empirically applicable in so far as one can estimate these interactions. The analysis then continues to explore the role of specific species in putative loss of coexistence. Desaillais et al. identify two species-level quantities: the first measures the total influence of the surrounding community on a focal species, while the second is a proxy for how close that focal species is to being lost, should a perturbation occur. While these two quantities are not mathematically independent, their correlation is not perfect, allowing one to categorize species into distinct ecological roles. A dataset of plant communities with different compositions illustrates how to apply this idea and gain some additional insight into the robustness of coexistence. These results pave the way for a number of potentially rewarding applications. How does the robustness of coexistence differ across network types? For which network types do we find back a more diverse set of ecological roles for species, i.e. for which networks are the two quantities least correlated?
References
1. Baert, J.M., Janssen, C.R., Sabbe, K., and De Laender, F. (2016). Per capita interactions and stress tolerance drive stress-induced changes in biodiversity effects on ecosystem functions. Nat. Commun. 7, 12486. https://doi.org/10.1038/ncomms12486
2. Pásztor, L., Botta-Dukat, Z., Magyar, G., Czaran, T., and Meszéna, G. (2016). Theory-based ecology: A Darwinian approach 1st ed. (Oxford University Press).
3. Cenci, S., Montero-Castaño, A., and Saavedra, S. (2018). Estimating the effect of the reorganization of interactions on the adaptability of species to changing environments. J. Theor. Biol. 437, 115–125. https://doi.org/10.1016/j.jtbi.2017.10.016
4. Spaak, J.W., Baert, J.M., Baird, D.J., Eisenhauer, N., Maltby, L., Pomati, F., Radchuk, V., Rohr, J.R., Van den Brink, P.J., and De Laender, F. (2017). Shifts of community composition and population density substantially affect ecosystem function despite invariant richness. Ecol. Lett. 20, 1315–1324. https://doi.org/10.1111/ele.12828
5. Meszéna, G., Gyllenberg, M., Pásztor, L., and Metz, J.A.J. (2006). Competitive exclusion and limiting similarity: A unified theory. Theor. Popul. Biol. 69, 68–87. https://doi.org/10.1016/j.tpb.2005.07.001
6. Saavedra, S., Rohr, R.P., Bascompte, J., Godoy, O., Kraft, N.J.B., and Levine, J.M. (2017). A structural approach for understanding multispecies coexistence. Ecol. Monogr. 87, 470–486. https://doi.org/10.1002/ecm.1263
7. Grilli, J., Adorisio, M., Suweis, S., Barabás, G., Banavar, J.R., Allesina, S., and Maritan, A. (2017). Feasibility and coexistence of large ecological communities. Nat. Commun. 8. https://doi.org/10.1038/ncomms14389
8. Desallais M, Loreau M, Arnoldi J.F. (2024) The distribution of distances to the edge of species coexistence. bioRxiv, ver.4 peer-reviewed and recommended by PCI Ecology https://doi.org/10.1101/2024.01.21.575550
DOI or URL of the preprint: https://doi.org/10.1101/2024.01.21.575550
Version of the preprint: 1
The manuscript “On the robustness of species coexistence to environmental perturbations” uses the geometrical concept of the feasibility domain to ask how much one can perturb intrinsic growth rates without losing species.
The focus of the paper is on the smallest perturbations that would push a community dangerously close to species loss. A first analysis gains some intuition with a 3-species case, showing that the proportion of growth rate vectors within a distance z of the feasibility domain’s edges is proportional to the radius of the largest disk one can fit in this feasibility domain. Next, this idea is extended to higher dimensions, showing how robustness (defined as the minimum amount of growth rate perturbation to cause extinction) depends on essentialy species interactions and species richness. Then, the probability of the distance to the feasibility domain’s edge is approximated for two different scenarios, and insight is gained on the contribution of individual species to robustness. Finally, there is an application of the theory to experimental data.
The three reviewers are overall positive and see the merit of this work, but also highlight some room for improvement. Most of these comments revolve around a more complete appraisal of similar efforts in this field (which may have gone unnoticed by the authors), a more careful pronunciation of one of the study’s premise (coexistence ensues if feasibility holds), and some numerical experiments to test how the theory predicts consequences of “real world” parameter perturbations.
I very much enjoyed this paper and agree with the reviewers it is an important step forward. However, I feel the section “Distribution of distances to the edge of feasibility” is quite technical and risks shooing away many generalist readers, appealing almost exclusively to scientists with the right mathematical chops. If this is the intended audience, fine for me, but I think the content of the paper merits a broader readership, as some of the implications of the results are potentially important (as explained very well in the excellent discussion). One approach could be to develop a more detailed/technical supp. document for people like me who want to understand every detail (which I was not able given only the main text) and then focus on the main equations and what they mean ecologically in the main text. Regarding literature that could be included in the intro or discussion, I spontaneously think of Cenci et al’s paper (10.1016/j.jtbi.2017.10.016) and our recent paper (https://onlinelibrary.wiley.com/doi/abs/10.1111/ele.14278), which both integrate environmental change into feasibility domain theory.
This work quantitatively evaluates the fragility of ecological communities to loose species given the size and shape of the feasibility domain. The wide adoption of the study of structural stability in ecology focus first on the size of the feasibility domain, which determines the range of opportunities for species to coexist (Rohr et al. 2014, Saavedra et al. 2017, Godoy et al. 2018). Aftwerwards, researchers realized the importance of the shape of such feasiblity domain for understanding species coexistence as not all species have equal probabilities to persist (Medeiros et al. 2021, Allen-Perkins et al. 2023, Lepori et al. 2024). This study follows this line of research evaluating the robustness of species coexistence to environmental perturbations.
The manuscript is well presented and the figures clarify the work, yet it does not reflect well in my opinion work that has done before. For instance, the abstract states that prior work has focused on understand the set of intrinsic growth rates compatible with species coexistence, while in this present work, the author ask the novel question: Given the fact that species coexist, which will be the minimal perturbation that changes this outcome. I am afraid other studies has answered already the same question including at least Allen-Perkins et al. 2023 ELE and Lepori et al. 2024 Proc Roy B. So the abstract needs to be reoriented in my opinion to better reflect the novelty of the work without diminish previous efforts.
Likewise, it is introduced that Allen-Perkins et al. (2023) has a promising direction yet not enough to test quantitative predictions regarding the robustness of species coexistence to actual perturbations (line 41). As coauthor of such paper I would like to express a different opinion. Actually, Allen-Perkins et al (2023) propose a metric called "Exclusion ratio" that actually measure distance to the edge of the feasbility domain according only to the interaction matrix that give an assymetric domain. In the exact same way as this work, it is considered that environmental perturbation affects species intrinsic growth rates considering an isometrix (non-directional) perturbation, and therefore, it evaluates what will be the minimal perturbation to reach the edge of the feasiblity domain and start to lose species. Note that such metric called exclusion ratio does not take into account a particular configuration according to an observed intrinsic growth rate, rather it focuses only in the structure of the matrix of interactions. See more detail in Box 1 and Fig. 2 of Allen-Perkins et al. (2023), and the isometric perturbation which is exactly the same approach as Fig. 2 of present work. Moreover, metrics of Allen-Perkins et al. 2023 (Box 1) also consider the difference in distance to the edge between an equilateral triangle and an non-equilateral one (Fig. 2 of present work as well as equations 7 and 8), and finally Allen-Perkins et al. (2023) also provide metrics to evaluate the robustness of species coexistence at both the individual species level and the entire community for an arbitraty number of species in the community. So unless I am missing something both approaches are alike or very simmilar, and a key aspect here is to clarify which part of the methodology represents a significant advance.
In my opinion, a key novel aspect compared to prior work is to classify species according to their competitive roles. I do like a lot the section about “Contextual species contributions to the robustness of coexistence” which provide a tractable analysis to see species through their competitive behaviour, therefore it can be seen which species play a central role for the coexistence of communities and which species can be considered as “disruptors”. This is really novel and interesting because can reduce the complexity we often observe in horizontal network to point out the importance of particular species. I can envision the importance of this work for applied fields such as restoration ecology, ecosistem functioing or species conservation.
Another point which I think is very interesting but in my opinion not well explained is the edge effects in high dimensions. That is the jump from larger distance to the edge to small distances. The authors put much importance in this result, but it is not well hilighted for the general reader, so it is hard to grasp which is the main finding. My take on this, and it is just a suggestion, is that the cumulative shape shows which will be the optimum number of species for random matrices at which there is a balance between gaining and losing species. At very high number of species as the author state a very small perturbation will make the community to loss species, while there will be an optimal point (by calculating the tagent) where species can maximize both diversity and the robustness against environmental perturbations.
Finally, the discussion section presents well the results, and provide nice discussion of the main findings and how this relates to prior work. I like the section when it is discussed that the environental perturbation was modelled as a perturbation that occur in all possible directions, and future work should focus on other types of environmental perturbation, including directional perturbation of changes of intrisinc growth rates in a given direction. A finally surprising fact is that many of the things that I have said before are acknowledged in the discussion section (lines 331-337), which seems odd to have this agreement at the end or not at the beginning. It seems that both works at some point where done simulateously without knowing from each other. I think there is a lot of room for more work on this geometric analysis of the feasibility domain, and the authors of this work are excellent researchers and they have ample material to highlight the novelty of their work. In sum, the classification of individual species according to their competitive roles, the implications fo these role for specific applied subjects, and the balance between diversity and tolerance to perturbations are key examples.
With that said, it is very exicing to read and see that geometric analyses of species interactions are gaining momentum to better understand the mechanisms of species coexistence and make predictions of future dynamics in the community, that different labs reach same conclusions independently and that there is room for more significant improvements.
Does the title clearly reflect the content of the article? Yes.
Does the abstract present the main findings of the study? Yes.
Are the research questions/[hypotheses]/predictions clearly presented? No.
Does the introduction build on relevant research in the field? Yes.
Are the methods and analyses sufficiently detailed to allow replication by other researchers? Yes.
Are the methods and statistical analyses appropriate and well described? Yes.
Are the results described and interpreted correctly? Yes.
Have the authors appropriately emphasized the strengths and limitations of their study/[theory]/methods/argument? No.
Are the conclusions adequately supported by the results (without overstating the implications of the findings)? Yes.
------
Based on previous theoretical and empirical studies on feasibility in ecology, Desallais et. al made an insightful step forward that tries to unravel the relationship between the robustness of a community and the geometrical properties of its feasibility domain. Specifically, they ask the question: how should we interpret perturbation in the scope of feasibility domains, what is the distribution of extinction-inducing perturbation intensity, and what is the relevant geometry properties governing such distribution?
Combing intuition in planar regular triangles and the analysis from previous closed-form results in multi-species feasibility domains, Desallais et. al were able to argue that for the distribution p(z), where z is the extinction-inducing perturbation intensity, two geometrical distances D* and D emerge as the relevant controlling parameter across all shapes and dimensions of feasibility domains. D*, the minimal extinction-inducing perturbation intensity, defines the characteristic scale of p(z). While D, another effective distance in unit of length, controls how fast p(z) grows from z=0 (boundary of feasibility domain).
----
The authors have stated their methodology carefully and overarching framework clearly. However, it is worth pointing out one major concern about potential lack of assumptions, since the feasibility domain is not equivalent to the domain where all species could coexist/persist. That is, it requires certain assumptions of stability to make them equivalent.
For some interaction matrix A, sampling some r inside the feasibility domain with some initial abundance N0, the corresponding system (r, A, N0) will have a feasible fixed point N, but such N may not be (locally) stable, and thus the loss of coexistence can occur in this system. Similarly, different initial abundances N0's may start the system in different basins of attraction, leading to different extinction outcomes. Chances are that the boarder of feasibility domains might not be the actual boarder of "coexistence domain". In this line, I haven't seen enough details that could validate the basics of how the authors would define robustness, also not in the empirical data analysis part. One possible workaround is to impose global stability for interaction matrices, cf. Deng et. al PloS Compt. Biol. 2022. Meanwhile, assumptions on stability may have already restricted the robustness properties, or exclude the system inferred in empirical analysis, which the authors may need to leverage.
------
The authors stated their research significance as "...move beyond a purely geometric description of the feasibility domain, and explicitly characterize the robustness..." in the introduction (line 45-46), and "unlike previous measures of asymmetry of the feasibility domain..., we included the notion of disturbance in the mathematical definition of z..." in the discussion (line 318). While I could totally see important contribution to this subject in this work, personally I would not perceive its significance this way. For previous work and this work are built on the similar feasibility-domain-geometry ground, and specifically, perturbation (parameter change) being mearsured geometrically as exceeding the feasibility domain seems to be a widely accepted conception in these works, as the authors already cited throughout their manuscript.
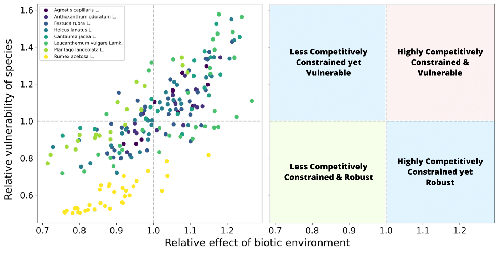
However, I do think this paper made a substantial step forward, in terms of providing an analytical approximation for the distribution of z, i.e, p(z). Such a distribution law, as mentioned by the authors, enables comparision across different interaction matrices and is thus universal knowledge for all systems. Moreover, it reveals the relevant geometrical parameters shaping this distribution. And to this end, we could be able to evaluate robustness across different systems in a consistent way, for example, a smaller z could be actually more robust than a larger z, solely because the first one lies in an "elongated" feasibility domain and the second one lies in a equilateral triangle feasibility domain; another example is the Figure 5 where one could immediately see how different communities operated at different status in terms of robustness.
------
Some minor points:
Personal summary:
This manuscript studies the robustness of the equilibria of a GLV model to perturbations on the growth rate of species. That is, given a feasible (but not necessarily stable) equilibria where all the species abundances are positive, they ask how big can a perturbation on the growth rates be until the first species abundance becomes negative. They embed the perturbation z in a function p(z) that is able to account for the geometry of the feasibility domain. In this way they are able to incorporate in their analysis both the sheer volume of such space, and its shape; an equally important factor in determining effective feasibility regions. The way they incorporate this shape information is by chipping away from the original feasibility region any volume that lies outside the the largest inscribed hypersphere with center given by the growth rate vector. That is, essentially the geometry is erased, collapsed to a hypersphere. Armed with this framework, they derive approximations to the distribution of hypersphere radii for general feasibility domains, and validate them by computing these radii for random parametrizations. Additionally, they also consider this analysis at the species level, computing a quantity called vulnerability to perturbation given coexistence, and another quantity called "how hostile the community is to species i". They then look at this quantities using parameter values derived in Barbier et al (2021) for grassland experiment data. This allows them to map experimental points onto their theory, providing an example of what type of insights this theory could give. The results make sense. A sensible, intuitive correlation is found: overall, species that perceive a hostile biotic environment are also the most vulnerable, pointing at the fact that this whole framework makes sense.
The manuscript seems to be technically sound, even though I was not able to check the math because I couldn't find the supplementary material. The results promise to be potentially useful. However, I have two major concerns that are preventing me from recommend this manuscript for publication.
Major concerns
Minor concerns
Title and Abstract
The title is vague because it does not state/hint to the main result of the paper.
The abstract presents how their theory generates new ways to study species contextual role in maintaining coexistence. In this sense, there is not a clear finding, but a proposal of a method/framework to look at data of species coexistence in a different way
Introduction
Materials and methods
I could not find the supplementary material with the links provided, so there are calculations and proofs that cannot be checked, or I have a hard time following (eq between lines 119 and 120, eqs 7, 8, 9, eqs between lines 168 and 169, eqs 10 and 11). The part of the paper where data is used makes use of parameters that are inferred in a different paper. This makes the whole data section hinge on results that are not reproducible with the information given in the paper.
See above answer. Nothe that this might be my problem, since I couldn't find the Supplementary Material
Results
Discussion
Refer to my first major concern.
 , 04 Mar 2024
, 04 Mar 2024Report of the data and script editor:
I could reply to all the questions below with a YES. The Jupiter notebook is extremely convenient and very well commented. This is a green light from my side.
1- Can we get the data and script from the links indicated in the submission form or from the article itself? Yes
2- Is there a readme file? Yes, the content of which is in the notebook.
3- Are there metadata for the data and comments for the scripts? Yes
4- Are the readme, and data files understandable by a normal reader? Yes
5- Do the scripts run on the data? Yes
6- Are the results the same as in the paper? Yes. (Not all figures of the article could directly be obtained from the script, but the author explained why in his latest reply, see the attached file. OK for me)