Understanding the effects of environmental perturbations on coexistence is a key challenge in ecology, and models have played an important role in structuring our ideas and generating predictions, leading to quantitative hypotheses. In such models, environmental perturbations are often captured by changes in parameter values, such as the intrinsic growth rates of species (1–3). The question then becomes how much one can change these parameters without breaking coexistence and thus losing species (4). 
 
An intuitively appealing approach to address this question is to calculate a model’s feasibility domain (5–7). Loosely defined, it is the fraction of parameter settings leading to the coexistence of all species. Mathematically speaking, it is a high-dimensional triangle, of which one can calculate the size, just as for plain two-dimensional triangles. Parameter settings outside of this triangle break coexistence. Thus, it seems logical that greater feasibility domains would make for more robust ecosystems. However, careful interpretation is key: a greater feasibility domain merely implies that across many attempts at running a model with different random parameter settings, coexistence will be more frequent. It does not necessarily inform us how much one can perturb the parameters of a community with a predefined parameter setting. To get this information, we also need to know the shape of the triangle (7): perturbations more easily knock the parameter setting out of a flat triangle than out of an equilateral triangle. 
 
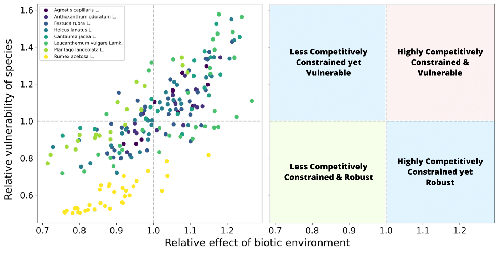
Desaillais et al. (8) develop a new theory that sheds light on what drives the shape of the feasibility domain. Specifically, they present the probability distribution that tells how close to the edge of the feasibility domain the parameter settings in that domain tend to be. For example, all points in a very flat triangle are close to its edge, while in an equilateral triangle, most points are safely stowed inside. The results show how, in a Lotka-Volterra model, the matrix of species interactions fully defines this distribution, which makes the technique empirically applicable in so far as one can estimate these interactions. The analysis then continues to explore the role of specific species in putative loss of coexistence. Desaillais et al. identify two species-level quantities: the first measures the total influence of the surrounding community on a focal species, while the second is a proxy for how close that focal species is to being lost, should a perturbation occur. While these two quantities are not mathematically independent, their correlation is not perfect, allowing one to categorize species into distinct ecological roles. A dataset of plant communities with different compositions illustrates how to apply this idea and gain some additional insight into the robustness of coexistence. These results pave the way for a number of potentially rewarding applications. How does the robustness of coexistence differ across network types? For which network types do we find back a more diverse set of ecological roles for species, i.e. for which networks are the two quantities least correlated? 

References

1. Baert, J.M., Janssen, C.R., Sabbe, K., and De Laender, F. (2016). Per capita interactions and stress tolerance drive stress-induced changes in biodiversity effects on ecosystem functions. Nat. Commun. 7, 12486. https://doi.org/10.1038/ncomms12486

2. Pásztor, L., Botta-Dukat, Z., Magyar, G., Czaran, T., and Meszéna, G. (2016). Theory-based ecology: A Darwinian approach 1st ed. (Oxford University Press).

3. Cenci, S., Montero-Castaño, A., and Saavedra, S. (2018). Estimating the effect of the reorganization of interactions on the adaptability of species to changing environments. J. Theor. Biol. 437, 115–125. https://doi.org/10.1016/j.jtbi.2017.10.016

4. Spaak, J.W., Baert, J.M., Baird, D.J., Eisenhauer, N., Maltby, L., Pomati, F., Radchuk, V., Rohr, J.R., Van den Brink, P.J., and De Laender, F. (2017). Shifts of community composition and population density substantially affect ecosystem function despite invariant richness. Ecol. Lett. 20, 1315–1324. https://doi.org/10.1111/ele.12828

5. Meszéna, G., Gyllenberg, M., Pásztor, L., and Metz, J.A.J. (2006). Competitive exclusion and limiting similarity: A unified theory. Theor. Popul. Biol. 69, 68–87. https://doi.org/10.1016/j.tpb.2005.07.001

6. Saavedra, S., Rohr, R.P., Bascompte, J., Godoy, O., Kraft, N.J.B., and Levine, J.M. (2017). A structural approach for understanding multispecies coexistence. Ecol. Monogr. 87, 470–486. https://doi.org/10.1002/ecm.1263

7. Grilli, J., Adorisio, M., Suweis, S., Barabás, G., Banavar, J.R., Allesina, S., and Maritan, A. (2017). Feasibility and coexistence of large ecological communities. Nat. Commun. 8. https://doi.org/10.1038/ncomms14389

8. Desallais M, Loreau M, Arnoldi J.F. (2024) The distribution of distances to the edge of species coexistence. bioRxiv, ver.4 peer-reviewed and recommended by PCI Ecology https://doi.org/10.1101/2024.01.21.575550