
BARABAS gyorgy
Recommendations: 0
Review: 1
Review: 1
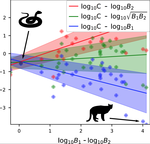
A macro-ecological approach to predators' functional response
A meta-analysis to infer generic predator functional response
Recommended by Samir Simon Suweis based on reviews by Ludek Berec and gyorgy barabasSpecies interactions are classically derived from the law of mass action: the probability that, for example, a predation event occurs is proportional to the product of the density of the prey and predator species. In order to describe how predator and prey species populations grow, is then necessary to introduce functional response, describing the intake rate of a consumer as a function of food (e.g. prey) density.
Linear functional responses shapes are typically introduced in the ecological modeling of population dynamics for both predator-prey and mutualistic systems [1,2]. Recently some works have proposed alternatives to the classic approach for mutualistic systems [3,4], both because cooperative interactions also model effect not directly related to mass action [3] and for analytical tractability [4,5].
In this work [6] the authors challenge the classic modeling of functional response also for predator-prey systems. In particular, they use a meta-analysis of several observational studies of predator-prey ecosystems to infer a generic predator functional response, fitting a phenomenological generalization of the mass-action law. Using advanced statistical analysis, they show that the functional response obtained from data is clearly different from the mass-action assumption. In fact, they found that it scales sub-linearly as the square root of the ratio between predator and prey biomass. They further argue that, from a macro-ecological point of view, using such a phenomenological relationship might be more valuable than relying on various mechanistic functional response formulations.
The manuscript thus provides an interesting different perspective on how to approach predator-prey modelling and for this reason, I have recommended the work for PCI Ecology.
References
[1] Volterra, V. (1928). Variations and Fluctuations of the Number of Individuals in Animal Species living together. ICES Journal of Marine Science, 3(1), 3–51. doi: 10.1093/icesjms/3.1.3
[2] Bastolla, U., Fortuna, M. A., Pascual-García, A., Ferrera, A., Luque, B., and Bascompte, J. (2009). The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature, 458(7241), 1018–1020. doi: 10.1038/nature07950
[3] Tu, C., Suweis, S., Grilli, J., Formentin, M., and Maritan, A. (2019). Reconciling cooperation, biodiversity and stability in complex ecological communities. Scientific Reports, 9(1), 1–10. doi: 10.1038/s41598-019-41614-2
[4] García-Algarra, J., Galeano, J., Pastor, J. M., Iriondo, J. M., and Ramasco, J. J. (2014). Rethinking the logistic approach for population dynamics of mutualistic interactions. Journal of Theoretical Biology, 363, 332–343. doi: 10.1016/j.jtbi.2014.08.039
[5] Suweis, S., Simini, F., Banavar, J. R., and Maritan, A. (2013). Emergence of structural and dynamical properties of ecological mutualistic networks. Nature, 500(7463), 449–452. doi: 10.1038/nature12438
[6] Barbier, M., Wojcik, L., and Loreau, M. (2020). A macro-ecological approach to predators’ functional response. BioRxiv, 832220, ver. 4 recommended and peer-reviewed by Peer Community in Ecology. doi: 10.1101/832220