

 based on reviews by Megan Griffiths and 2 anonymous reviewers
based on reviews by Megan Griffiths and 2 anonymous reviewers
Although monitoring the prevalence of pathogens in wildlife is crucial, there are logistical constraints that make this difficult, costly, and unpractical. This problem is often compounded when attempting to measure the temporal dynamics of prevalence. To improve the detection rate, a commonly used technique is pooling samples, where multiple individuals are analyzed at once. Yet, this introduces further potential biases: low-prevalence samples are effectively diluted through pooling, creating a false negative risk; negative samples are masked by the inclusion of positive samples, possibly artificially inflating the estimate of prevalence (and masking the inter-sample variability).
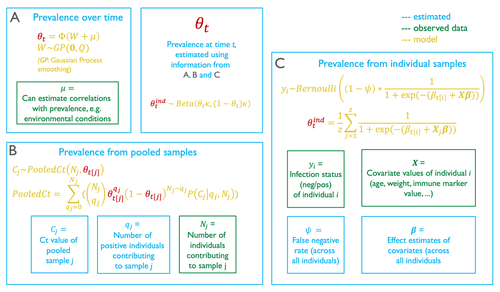
In their contribution, Borremans et al. (2024) come up with a modelling technique to provide accurate predictions of prevalence dynamics using a mix of pooled and individual samples. Because this model represents the pooling of individual samples as a complete mixing process, it can accurately estimate the prevalence dynamics from pooled samples only.
It is particularly noteworthy that the model provides an estimation of the false negative rate of the test. When there are false negatives (or more accurately, when the true rate at which false negatives happens), the value of the effect coefficients for individual-level covariates are likely to be off, potentially by a substantial amount. But besides more accurate coefficient estimation, the actual false negative rate is important information about the overall performance of the infection test.
The model described in this article also allows for a numerical calculation of the probability density function of infection. It is worth spending some time on how this is achieved, as I found the approach relying on combinatorics to be particularly interesting. When pooling, both the number of individuals that are mixed is known, and so is the measurement made on the pooled samples. The question is to figure out the number of individuals that because they are infectious, contribute to this score. The approach used by the authors is to draw (with replacement) possible positive and negative test outcomes assuming a number of positive individuals, and from this to estimate a pathogen concentration in the positive samples. This pathogen concentration can be transformed into its test outcome, and this value taken over all possible combinations is a conditional estimate of the test outcome, knowing the number of pooled individuals, and estimating the number of positive ones.
This approach is where the use of individual samples informs the model: by providing additional corrections for the relative volume of sample each individual provides, and by informing the transformation of test values into virus concentrations.
The authors make a strong case that their model can provide robust estimates of prevalence even in the presence of common field epidemiology pitfalls, and notably incomplete individual-level information. More importantly, because the model can work from pooled samples only, it gives additional value to samples that would otherwise have been discarded because they did not allow for prevalence estimates.
References
Benny Borremans, Caylee A. Falvo, Daniel E. Crowley, Andrew Hoegh, James O. Lloyd-Smith, Alison J. Peel, Olivier Restif, Manuel Ruiz-Aravena, Raina K. Plowright (2024) Reconstructing prevalence dynamics of wildlife pathogens from pooled and individual samples. bioRxiv, ver.3 peer-reviewed and recommended by PCI Ecology https://doi.org/10.1101/2023.11.02.565200
DOI or URL of the preprint: https://doi.org/10.1101/2023.11.02.565200
Version of the preprint: 2
 , posted 26 Mar 2024, validated 28 Mar 2024
, posted 26 Mar 2024, validated 28 Mar 2024Both reviewers recognize the improvements made to the manuscript after this round of revision. One of the reviewers is concerned about the fact that changes to eq. 1-2 requires additional simulations and discussion; after reading their review, I tend to share this concern, and I am expecting the revised version to address these comments in detail.
 , 28 Feb 2024
, 28 Feb 2024The authors have successfully addressed all of my comments and I believe that the manuscript is improved in both content and readability. I am happy for the manscript to be accepted in this state.
The changes the authors make have greatly improved the manuscript. The extra information and clarification they provide address all of my comments. However, the additional information they provide about equations 1 and 2 make it clear that the model formulation must be remedied before publication. This will require rerunning simulations, etc. since the model will need to be refit following reformulation. As it is written, unfortunately the model is not mathematically well defined, leading to potentially incoherent situations. For example, if you want to simulate data for a population in which prevalence is equal to 0, but simultaneously all members of the population have a covariate value that is known to perfectly correlate with disease, then you have a problem. The prevalence parameter implies all y_i should equal 0, while the covariate implies all y_i should be equal to 1. The model needs to avoid such mathematically pathological situations, and it is unreasonable to simply advise against use in such scenarios in a discussion section for more substantial reasons described below.
Standard probability rules require a random variable to have a single definition. Defining it twice, as the authors do via equations 1 and 2 is not a valid way to specify a joint probability model. The authors may only specify a single Bernoulli distribution for y_i. The authors must explicitly write mathematically, in an equation, how they wish the individual-level covariates to interact or otherwise relate to population-level prevalence. Although it is simple to write a single equation involving both theta and the covariates, the revision could potentially place the population-level prevalence term in tension with the effect of individual level covariates. Naturally, population-level prevalence partly arises from the aggregate effects of individual-level risks and outcomes. A revision will likely require some careful thinking about how to (re?)interpret model parameters.
Statistical software may or may not enforce the one definition rule, but that does not justify ignoring it. For example, while the R software Stan may interpret multiple definitions for a random variable as a user’s request to make two separate contributions for the variable to the log-likelihood, the R software Nimble refuses to build models when variables are defined twice. In general, statistical software is not necessarily provided with guard rails to prevent users from doing “prohibited” things. Drawing on an example commonly taught in introductory regression modeling classes, the R function lm() (and equivalent functions in other statistical software, like SASS) will let users fit a least squares linear regression model to binary data, even though users should use logistic regression models (or similar) to fit binary data. When software provides estimates for models that are not mathematically well defined, the estimates in general will not be able to be interpreted in the way users intend. Software predictions may also be non-sensible, which is the main concern with fitting binary data to a least square linear regression.
DOI or URL of the preprint: https://doi.org/10.1101/2023.11.02.565200
Version of the preprint: 1
 , posted 09 Jan 2024, validated 09 Jan 2024
, posted 09 Jan 2024, validated 09 Jan 2024Both reviewers are generally very supportive of the work, and make specific suggestions to improve the presentation. After reading the preprint and the reviewer comments, I find myself in agreement with their feedback. It should be possible for the authors to incorporate all of it in a revision.
This study describes a new computational approach for obtaining viral prevalence estimates using naturally pooled samples, the use of which is currently limited to presence/absence information in an area.
The methods presented represent a significant advance in the analysis of pooled samples and have the potential to allow the study of pathogen prevalence in wildlife populations without the time, expense, and hazard of catching and handling individual animals. Where individual level samples are also available, the authors include methods for directly incorporating individual covariates. The true prevalence over time section of the model offers the potential to, although not explored by the authors, directly incorporate a transmission model and fit these parameters which should allow for the direct combining of uncertainty from the other sections of the model. The discussion provides a fair assessment of the potential utility of the model whilst discussing its limitations, specific requirements, and drawbacks.
Whilst the authors explore a good range of non-ideal data scenarios, I am not convinced that these scenarios reflect a ‘realistic’ dataset. I would like to see if the close match to the simulated prevalence is maintained when multiple potentially confounding factors are combined, i.e., small and varying sample sizes, taken at irregular intervals. I would recommend not overstating the realism of the test data in the discussion.
Below are some suggestions for clarifications of the text and figures.
I’m not sure of the length allowances for the abstract in this journal, but I find the abstract rather long, which detracts rather than enhances interest in the article.
The introduction describes in detail the current state of the field, and the need for the model. The research question is clearly presented but could again be more concise for readability.
Figure 1 – The black lines on the figure showing the connectivity between the sections aren’t very informative and I think make things less clear. That the relevant parameter is highlighted in a different colour is enough to see that it occurs in all three sections. Perhaps make it bold as well if the colour alone is not clear enough. Is θ observed as per the key? Is that not what all sections of the model come together to estimate? If the important thing is that it’s estimated by all of them, put it outside of the other boxes.
Should equation 2 match the relevant equation in figure 1 (currently the yellow equation in box C)?
Page 10 line 5 – the three key factors that influence final pooled concentration. You mention a few paragraphs later than urine volume is assumed to be equal, but on first read-through I was wondering in this section why it was being ignored. A simple line of ‘here we focus on these first two factors’ would do to make readers stop wondering where the third one was!
Where laboratory experiments are required to determine distributions/baseline values should be clarified.
Add to the discussion on pool size limitations of this method that this should be taken into account during the field experimental design and set-up if feasible for most reliable results. Possibly mention that this is more suitable for some wildlife species than others given their usual behaviours and living arrangements.
Figure 2 – Would add either in the figure or the legend, how these steps (A-D) relate to the numbered steps in the main text. Am I understanding correctly that example in this figure (Ct 36, 2/3 bats/ 20% prevalence) is randomly chosen, and that this process would need to be completed for all possible combinations? If so, add a final line in the legend stating this?
Figure 4 – I think that the 50% CI shading should stand out a bit more. I would also recommend moving the datapoints to the top layer of the figure so that they are not hidden behind the fitted prevalence curves or the credible interval band.