

Barbier et al. (2024) investigated the dynamics of species abundances depending on their ecological niche (abiotic component) and on (numerous) competitive interactions. In line with previous evidence and expectations (Barbier et al. 2018), the authors show that it is possible to robustly infer the mean and variance of interaction coefficients from species co-distributions, while it is not possible to infer the individual coefficient values.
The authors devised a simulation framework representing multispecies dynamics in an heterogeneous environmental context (2D grid landscape). They used a Lotka-Volterra framework involving pairwise interaction coefficients and species-specific carrying capacities. These capacities depend on how well the species niche matches the local environmental conditions, through a Gaussian function of the distance of the species niche centers to the local environmental values.
They considered two contrasted scenarios denoted as « Environmental tracking » and « Dispersal limited ». In the latter case, species are initially seeded over the environmental grid and cannot disperse to other cells, while in the former case they can disperse and possibly be more performant in other cells.
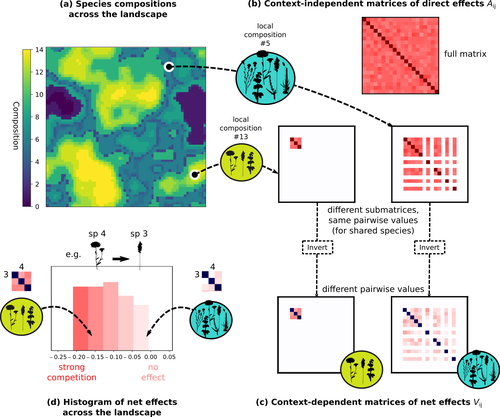
The direct effects of species on one another are encoded in an interaction matrix A, and the authors further considered net interactions depending on the inverse of the matrix of direct interactions (Zelnik et al., 2024). The net effects are context-dependent, i.e., it involves the environment-dependent biotic capacities, even through the interaction terms can be defined between species as independent from local environment.
The results presented here underline that the outcome of many individual competitive interactions can only be understood in terms of macroscopic properties. In essence, the results here echoe the mean field theories that investigate the dynamics of average ecological properties instead of the microscopic components (e.g., McKane et al. 2000). In a philosophical perspective, community ecology has long struggled with analyzing and inferring local determinants of species coexistence from species co-occurrence patterns, so that it was claimed that no universal laws can be derived in the discipline (Lawton 1999). Using different and complementary methods and perspectives, recent research has also shown that species assembly parameter values cannot be unambiguously inferred from species co-occurrences only, even in simple designs where an equilibrium can be reached (Poggiato et al. 2021). Although the roles of high-order competitive interactions and intransivity can lead to species coexistence, the simple view of a single loop of competitive interactions is easily challenged when further interactions and complexity is added (Gallien et al. 2024). But should we put so much emphasis on inferring individual interaction coefficients? In a quest to understand the emerging properties of elementary processes, ecological theory could go forward with a more macroscopic analysis and understanding of species coexistence in many communities.
The authors referred several times to an interesting paper from Schaffer (1981), entitled « Ecological abstraction: the consequences of reduced dimensionality in ecological models ». It proposes that estimating individual species competition coefficients is not possible, but that competition can be assessed at the coarser level of organisation, i.e., between ecological guilds. This idea implies that the dimensionality of the competition equations should be greatly reduced to become tractable in practice. Taking together this claim with the results of the present Barbier et al. (2024) paper, it becomes clearer that the nature of competitive interactions can be addressed through « abstracted » quantities, as those of guilds or the moments of the individual competition coefficients (here the average and the standard deviation).
Therefore the scope of Barbier et al. (2024) framework goes beyond statistical issues in parameter inference, but question the way we must think and represent the numerous competitive interactions in a simplified and robust way.
References
Barbier, Matthieu, Jean-François Arnoldi, Guy Bunin, et Michel Loreau. 2018. « Generic assembly patterns in complex ecological communities ». Proceedings of the National Academy of Sciences 115 (9): 2156‑61. https://doi.org/10.1073/pnas.1710352115
Barbier, Matthieu, Guy Bunin, et Mathew A Leibold. 2024. « Getting More by Asking for Less: Linking Species Interactions to Species Co-Distributions in Metacommunities ». bioRxiv, ver. 2 peer-reviewed and recommended by Peer Community in Ecology. https://doi.org/10.1101/2023.06.04.543606
Gallien, Laure, Maude Charlie Cavaliere, Marie Charlotte Grange, François Munoz, et Tamara Münkemüller. 2024. « Intransitive stability collapses under the influence of dominant competitors ». The American Naturalist. https://doi.org/10.1086/730297
Lawton, J. H. 1999. « Are There General Laws in Ecology? » Oikos 84 (février):177‑92. https://doi.org/10.2307/3546712
McKane, Alan, David Alonso, et Ricard V Solé. 2000. « Mean-field stochastic theory for species-rich assembled communities ». Physical Review E 62 (6): 8466. https://doi.org/10.1103/PhysRevE.62.8466
Poggiato, Giovanni, Tamara Münkemüller, Daria Bystrova, Julyan Arbel, James S. Clark, et Wilfried Thuiller. 2021. « On the Interpretations of Joint Modeling in Community Ecology ». Trends in Ecology & Evolution. https://doi.org/10.1016/j.tree.2021.01.002
Schaffer, William M. 1981. « Ecological abstraction: the consequences of reduced dimensionality in ecological models ». Ecological monographs 51 (4): 383‑401. https://doi.org/10.2307/2937321
Zelnik, Yuval R., Nuria Galiana, Matthieu Barbier, Michel Loreau, Eric Galbraith, et Jean-François Arnoldi. 2024. « How collectively integrated are ecological communities? » Ecology Letters 27 (1): e14358. https://doi.org/10.1111/ele.14358
DOI or URL of the preprint: https://doi.org/10.1101/2023.06.04.543606
Version of the preprint: 2
 , posted 04 Dec 2023, validated 06 Dec 2023
, posted 04 Dec 2023, validated 06 Dec 2023Dear colleagues,
First and foremost, I want to congratulate you for the excellent work you have done. The context, objectives and results, as well as the future challenges, are very clearly presented in this manuscript. The discussion and the conclusions are sound and should inspire future other works on this topic. The Figures are all useful and nice, and the text reads very well.
As you will see below, three reviewers have assessed your manuscript.
They have provided a number of relevant comments and suggestions.
Therefore, I propose that you prepare and submit a new version of the manuscript that carefully consider all the reviewers' points.
We look forward to reading the new version of the manuscript.
Best wishes,
François
 , 30 Nov 2023
, 30 Nov 2023This manuscript explores the limits of accurately inferring biotic interaction strength and direction from datasets that are simulated to mimic certain field conditions. The authors answered a common logistical question in community ecology: when can we infer more from sparse data? They provided clear results showing that inference will be more challenging when species are not dispersal limited, but even then the mean and/or variance of the inferred interaction matrix may still be reliable.
I have found the paper very clearly written, and the figures are well-annotated and relatively accessible to a general audience. The Methods text may need a bit more clarity to guide us through the steps (e.g., at times I was not sure how inference was made / how models were fitted on the simulated data; do the mathematical equations describe either or both the simulation and inference?), but there was nothing major that prevents a reader like me from grasping the full picture.
Here are some specific comments:
For a reader like me who is a frequent user of joint species distribution model (or think in that framework), several of the cited papers in this manuscript keep leaving me a lingering thought "so what does this mean to my JSDM or co-distribution datasets?" The authors did quite a good job outlining JSDMs in paragraph 3, as well as their shortcomings citing Poggiato et al. 2021, but in the Discussion I find myself still hungry for more insights from the authors. From here I learned that dispersal limitation (or the lack thereof) is key to whether the results from JSDMs are reliable in inferring biotic interaction, but which results is it from a JSDM? As a user of JSDMs, it is still unclear to me whether we could reliable interpret the latent associations (or residual components) as biotic interactions / associations not accounted for by the environment (assuming that we have measured all the important abiotic covariates), or do we include neighbour densities as measured covariates. Knowing Leibold et al. (2022) Oikos, I was waiting for a bit more insights into the way forward to use JSDMs. Of course, not everything needs to be analysed as a JSDM (or using existing JSDM softwares). Maybe this is why the authors opted not be too overprescriptive. It is just that the regular JSDM citations leave one hanging about them. I apologise for not having any concrete solution to suggest at this moment.
The second point is about the term non-additivity sprikled throughtout this work. I appreciate the authors noting this, but it isn't clear to me whether they think non-addivity is something to avoid, or something to tackle. In the 3rd Discussion paragraph, I learned that non-addivities (or indirect effect) may be more prevalent in the environment-tracking scenario or when most species have reached equilibrium, so do well avoid ill-posed questions under these situations? Or would the inclusion of N_j by E(x) interaction term in a statistical model be the first step to account for non-additivities? I am not expecting a lengthy response but only exploring if the authors have clearer suggestions for this, as I understand that this may not fit within the scope of the current work.
I appreciate the effort going into explaining complex terminologies and concepts, but there are still a few places that could be more spelled out to help us understand. For example:
- In the 5th Intro paragraph, you may need to guide us through direct to net interactions. Why does the inverse tell us the net effects? When we say inverse of the community matrix, what exactly is a community matrix. To some community ecologists, it is the site-species matrix, which is definitely not what the authors meant here.
- The term "disordered interactions" are coined multiple times, but during the Intro I wasn't left hanging until reading it again in the Discussion. Can it be defined more early on?
- In the last Intro paragraph, what does "dynamical regime of species sorting" mean?
- Does the last summation term (N of y - N of x) imply mass effect?
- Figure 1e is interesting. Do you think it is true / would help to highlight that the dispersal limitation on more superiour competitors is also crucial to the persistence of an inferior focal species in a patch?
- Perhaps refer to Equation 2 in Section 1.4, because I found it confusing what the actual inference is.
Then, throughout the manuscript I constantly thought about multicollinearity, from a data perspective. I am not able to pinpoint this to any place of the manuscript, but let's say the 2nd Discussion paragraph. Here the authors mentioned "...if the same environmental conditions predictably lead to the same species composition..." Under environmental tracking, if one sample communities in the field they would need to face strong autocorrelation / multicollinarity between neighbour densities and the abiotic covariates. Is this true in the authors' simulated data too? Is this the statistical phenomenon that leads to confounding variables / non-indentifiability during the inference process? These are the questions that haunts my sleep whenever I fit a model including both neighbour densities and environment, so I wonder if the authors have any insights. From the top of my head, I also couldn't think of any literature that points out that aggregated statistics may be robust against multicollinearity even when individual coefficients are not, so I wonder if this is another way of highlighting the novel contribution of this work.
The text on equilibrium and "letting indirect effect play out" in the Discussion is really insightful; I hope it was highlighted more clearly / early on.
Thank you.
In the manuscript “Getting More by Asking for Less: Linking Species Interactions to Species Co-Distributions in Metacommunities”, the authors ask if one can infer species interactions from spatial occurrence data. More specifically, they first create such data by running a metacommunity model with a known species interaction matrix and then try to recover that matrix using regression techniques, as one would do when mining empirical data. Because their model considers the simplest of cases (linear per-capita growth, homogeneous dispersal), the test of inferential capacity is assumed to be generous and comradely: applying more complicated models can only lead to poorer results. Overall, they find that predictions of the whole species interaction matrix are poor, while estimates of its first two moments are more accurate. In general, the manuscript is very well written, the setup is smart, and the results are novel and (as far as I can see) correct.
I have the following comments:
1.1: “their abundances are set to zero, and only allowed to vary if their net growth rate dlogNi/dt becomes positive”. At first, confusing to me (I guess the verb “vary” got me sidetracked).
As I understand the simulation protocol, there is no regional equivalence: some species are inherently more fit than others. Intuitively (but I did not think this through properly), I’d say regional equivalence without dispersal (species do differ at the pixel level, but each species persists in the same fraction of pixels) affects inference of species interactions because it affects to what extent the landscape represents the experiment one would need to infer interactions.
I wonder why species in the dispersal limited case were only seeded in 50% of the patches. I’d think that seeding them everywhere (in combination to regional equivalence) can produce patterns that permit more reliable inference.
I have the same intuition as the authors that more complex models (displaying more complex dynamics) will not improve inference. However, I’m not sure how model complexity influences inferential capacity vs. simply the number of species (assuming the objective is to parameterize each and every specific interaction using field data). For any model, the number of parameters to estimate would scale exponentially with the number of species, and so one needs a larger design to identify them. If there is a lower limit to inferential capacity, one could ask if inference in large systems will hit rock bottom just the same in complex as in simple models. I’m not suggesting this issue be addressed in this paper, I’m just proposing the authors to ponder this thought.
The direct and indirect effects are interesting and I think identical to the definitions of Zelnik et al (https://doi.org/10.1101/2022.12.29.522189), so it may be useful to refer to that paper in section 1.3.
It might be worthwhile to discuss in what practical applications it would it be sufficient to know only the statistical properties of the interaction matrix, and what these first two moments could tell us about the system’s dynamic behavior and longer-term outcome. In other words: does what one gets (by asking for less) address one’s needs?
Fig1: very nice figure; maybe try to find a way to highlight that the tiles in the lower panel are results for different species.
Fig4: I don’t think the color codes are needed for stdA.