

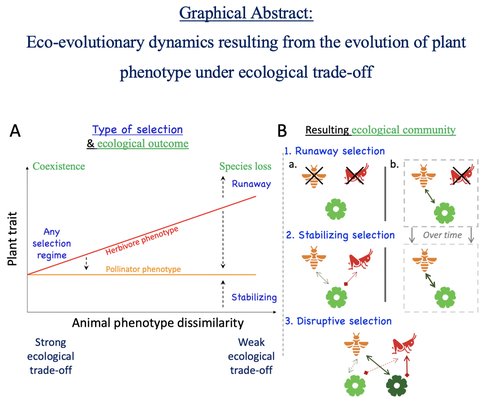
How would a plant trait evolve if it is involved in interacting with both a pollinator and an herbivore species? The answer by Yacine and Loeuille is straightforward: it is not trivial, but it can explain many situations found in natural populations.
Yacine and Loeuille applied the well-known Adaptive Dynamics framework to a system with three interacting protagonists: a herbivore, a pollinator, and a plant. The evolution of a plant trait is followed under the assumption that it regulates the frequency of interaction with the two other species. As one can imagine, that is where problems begin: interacting more with pollinators seems good, but what if at the same time it implies interacting more with herbivores? And that's not a silly idea, as there are many cases where herbivores and pollinators share the same cues to detect plants, such as colors or chemical compounds.
They found that depending on the trade-off between the two types of interactions and their density-dependent effects on plant fitness, the possible joint ecological and evolutionary outcomes are numerous. When herbivory prevails, evolution can make the ménage-à-trois ecologically unstable, as one or even two species can go extinct, leaving the plant alone. Evolution can also make the coexistence of the three species more stable when pollination services prevail, or lead to the appearance of a second plant species through branching diversification of the plant trait when herbivory and pollination are balanced.
Yacine and Loeuille did not only limit themselves to saying "it is possible," but they also did much work evaluating when each evolutionary outcome would occur. They numerically explored in great detail the adaptive landscape of the plant trait for a large range of parameter values. They showed that the global picture is overall robust to parameter variations, strengthening the plausibility that the evolution of a trait involved in antagonistic interactions can explain many of the correlations between plant and animal traits or phylogenies found in nature.
Are we really there yet? Of course not, as some assumptions of the model certainly limit its scope. Are there really cases where plants' traits evolve much faster than herbivores' and pollinators' traits? Certainly not, but the model is so general that it can apply to any analogous system where one species is caught between a mutualistic and a predator species, including potential species that evolve much faster than the two others. And even though this limitation might cast doubt on the generality of the model's predictions, studying a system where a species' trait and a preference trait coevolve is possible, as other models have already been studied (see Fritsch et al. 2021 for a review in the case of evolution in food webs). We can bet this is the next step taken by Yacine and Loeuille in a similar framework with the same fundamental model, promising fascinating results, especially regarding the evolution of complex communities when species can accumulate after evolutionary branchings.
Relaxing another assumption seems more challenging as it would certainly need to change the model itself: interacting species generally do not play fixed roles, as being mutualistic or antagonistic might generally be density-dependent (Holland and DeAngelis 2010). How would the exchange of resources between three interacting species evolve? It is an open question.
References
Fritsch, C., Billiard, S., & Champagnat, N. (2021). Identifying conversion efficiency as a key mechanism underlying food webs adaptive evolution: a step forward, or backward? Oikos, 130(6), 904-930.
https://doi.org/10.1111/oik.07421
Holland, J. N., & DeAngelis, D. L. (2010). A consumer-resource approach to the density‐dependent population dynamics of mutualism. Ecology, 91(5), 1286-1295.
https://doi.org/10.1890/09-1163.1
Yacine, Y., & Loeuille, N. (2024) Attracting pollinators vs escaping herbivores: eco-evolutionary dynamics of plants confronted with an ecological trade-off. bioRxiv 2021.12.02.470900; doi: https://doi.org/10.1101/2021.12.02.470900
DOI or URL of the preprint: https://doi.org/10.1101/2021.12.02.470900
Version of the preprint: 3
 , posted 24 Jan 2024, validated 24 Jan 2024
, posted 24 Jan 2024, validated 24 Jan 2024Dear colleagues,
two reviewers and myself have read the new version of your manuscript. We all agree that you did a very good work in responding our comments and modifying your manuscript after our suggestions.
I think we are close to a definitive version, pending you can answer the last comments of the reviewers, especially the one of reviewer 2 regarding the weakness of the way your model is built.
I recommend to follow reviewer 2's suggestion: either to modify your model fixing this flaw and assess whether it qualitatively changes your results (maybe in a small but significant parameter ranges), or to at least pinpoint the weakness, discuss it and make the reader aware of it. I think in addition to reviewer 2, that you have to explicitly write in the main text that such "unbounded growth regions" exist, and how you managed them for the study of the evolutionary trajectories. In particular, as the adaptive dynamics framework assumes the community to be ecologically stable when the mutant is introduced, it is unclear how you did your analysis in unbounded growth regions (i.e. if I am not wrong where P*, M*, H* do not exist). You can certainly avoid them as initial conditions, of course, but the difficulty especially rises when evolutionary trajectories would lead the community to such unbounded growth regions.
Hence, in order for your paper to be of high quality and to be appreciated in the long run by both theoreticians and empiricists, I would recommend that you modify your model in such a way to remove this flaw, check whether it has strong implication for your results in a limited parameter range, or at least make this limitation explicit and describe better how you dealt with it. Otherwise, I am afraid it would limit the impact of your paper and results.
Best regards,
Pr. Sylvain Billiard
Comments to the MS by Yacine & Loueille
I thank the authors for taking into account may suggestions about their MS. I only have a few minor suggestions for improving clarity.
1. If this model is not suitable for extreme cases in which the pollinator and the herbivore are the same species, it is worth mentioning it early in the description of the model, e.g., when the Lotka-Volterra equations are provided. Empirical pollination biologists will appreciate this clarification, because the study of "nursing pollination" is a hot topic in pollination biology.
2. About match of phenotypes, I appreciate the clarifications of the authors. I understand that authors prefer to use a terminology which allows broader interpretations, to gain generality. However, I believe that it is clearer, and equally broad, to talk about a match between plant phenotypes and animal preferences (instead of animal phenotypes). Talking about dissimilarity in preferences of pollinators and herbivores would definitely improve clarity for empirical pollination biologists (e.g. in the first mention of animal phenotypes on L. 139). Please, consider changing animal phenotype to animal preference.
3. Thanks for explicitely including reference to your previous modeling efforts. I wonder if this reference should be placed before the paragraph in which you state your goals. I believe readers will understand better the novelty of your model if the results of the previous model are introduced earlier.
4. A final comment, hopefully not too picky, is that your paragraphs in the Introduction are almost one page long, which can decrease readability. In particular, the last paragraph is over a page long. Please, try to split it or reducing its length.
Sincerely,
Marcos Méndez
January 2024
https://doi.org/10.24072/pci.ecology.100530.rev21I think the Authors did a good job addressing most of the comments from the previous round of reviews. Nevertheless, it appears that one issue persisted.
I wrote in my previour review, perhaps not in entirely clear terms, that the model defined by Eqs. 1 has a serious design flaw: When the conversion coefficient e_m and the rate a_{pm} are sufficiently large compared to the corresponding quadratic "death" rates c_m and c_p, both P and M catalyze each other and grow indefinitely. In terms of "natural" variables, it definitely makes no sense: No matter how well-pollinated a plant is, neither the plant nor the pollinator can increase their densities indefinitely.
I also suggested one of infinitely many possible ways to fix this flaw, preserving the phemonology similar to what is observed in the regime when the divergence is absent and ensures convergence for all values of the rates. Naturally, I have not expected the simulations and adaptive dynamics analysis to be redone to correct this flaw, but I insist that it has to be acknowledged. Writing in resubmission letter that "Other published theoretical works (e.g. Thébault & Fontaine 2010) have made similar assumptions." seems like a lame excuse for a pure theoretical work. So I strongly suggest to replace the vague terms "unstable community dynamics" and "unbound growth" in lines 445, 452 and Fig. 5 by something more self-critical, as, for example, "failure of the model", explain it and propose ways to fix it in the Discussion.
I see this issue as important and easily fixable, and making the discussion about it public appears to me as one of the merits of transparency of the new reviewing protocol.
https://doi.org/10.24072/pci.ecology.100530.rev22DOI or URL of the preprint: https://doi.org/10.1101/2021.12.02.470900
Version of the preprint: 2
 , posted 02 Jun 2023, validated 05 Jun 2023
, posted 02 Jun 2023, validated 05 Jun 2023Dear Youssef and Nicolas,
I received two reports, one from an empirical ecologist and the other from a theoretical ecologist. They both found your paper has merits but suggested some clarifications and modifications. As the reviewers, I particularly appreciated the way you thoroughly analysed you model, with multiple complementary approaches.
I concur with the referees' opinion and would be happy to recommend your paper pending some revisions. Please find below the issues that should be addressed in particular, based on my own reading of your paper and on the referees' reports.
Best regards,
Sylvain Billiard
I am very sorry for the delay.
The manuscript 'Attracting pollinators vs escaping herbivores: eco-evolutionary dynamics of plants confronted with an ecological trade-off'' presents a very thorough analysis of an eco-evolutionary model of 3 species: a prey, prey's cooperator, and a predator. Apparently for definity, these species are designated as flowering plants, their pollinators, and herbivores. The model is phenotype-based and only prey can evolve. A "tradeoff'' is defined as what occurs in a scenario when the selection pressures on the plant phenotype from the pollinator and herbivore act in opposite directions. The Authors present the quite intuitive adaptive dynamics prediction of the various evolutionary regimes and then confirm and build on the intuitive predictions doing a complete numerical sampling of the multidimensional parameter space of the model. And a special praise should be given to the clarity and excellent organization of the Supplementary Materials.
That all said, there are several serious drawbacks of the manuscript that to some extent devaluate its merits.
The first, and apparently the easy fixable one is to be more precise with the term ``tradeoff''. This word has become quite loaded and a reader, seeing it in the Title, first lines of the Abstract, and then numerously in the Introduction could quite feasibly be left puzzled by how the tradeoff is played out in the model. I suggest to move the explanation from the first paragraphs of Appendix B to the main text to make the definition of tradeoff more specific and precise. I would also look for perhaps more wordy yet more specific definition of the main quest of the manuscript very early in the text.
Second, way more attention should be given to the quantitative definition of the model. What are the meanings of the logistic (negative quadratic) terms for the pollinator and herbivore? Do those species compete for space? Such a term is essential for the stability of the model and could also be biologically justified for the plant, but why for the animals? The ``orgy'', coyly mentioned in the main text, which apparently is way better described as ``unlimited population growth'' in the Supplementary materials, could be totally avoided by making the plant birth rate saturating in the limit of the infinite population of pollinator. I think this is totally justified empirically and could be implemented in a multitude of ways, for example, defining the per capita birth rate as r_p*(1-c*exp(-a_{pm}*M). This or any other realistic definition of the limited plant birth rate will also make the c_m and c_h terms unnecessary for the stability.\( \)
Third. Unfortunately, it is assumed that the plant evolution has no cost, that is, the plant's phenotype can change indefinitely without affecting the plant's birth and death rates. Besides being totally unrealistic biologically, this assumption also results in evolutionary regimes, such as a runway evolution, that will not be possible if the plant phenotype were confined to an ecologically ``liveable'' interval. Again, there are many simple and ``canonical'' ways to take the ecological costs of changing phenotype into account, i.e. phenotype-dependent birth rate r_p or carrying capacity (1/c_p) that have a single (or even several) maxima and decay to zero away from those maxima.
Forth, are there any justifications for fixing the phenotypes of both animal species? Is it justified empirically? Are there any differences between animal/insect and plant genetics explaining that? A saying goes that a predator is evolutionary doomed if it evolved slower than its prey. In the presented work, in several scenarios the doom is circumnavigated by confining the prey phenotype to the favourable for the predator zone via its attraction to the pollination optimum. Allowing all three phenotypes to evolve will dramatically alter the evolutionary and ecological ``phase diagrams'', resulting in many non-stationary scenarios.
Given that I'm not reviewing the manuscript for any particular journal, I don't think I am in a position to make requests about the last 3 limitations. At the same time, I feel that independent of the target journal, those issues should be thoroughly discussed. Presumably, the authors have accumulated a lot of intuition about the model's dynamics that could allow them to qualitatively discuss what happens in more general cases that are free of those assumptions.
https://doi.org/10.24072/pci.ecology.100530.rev12